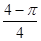题目内容
 P是边长为4的正方形ABCD所在平面外一点,AP=2,且AP与平面ABCD成45°角,则CP的最小值为
P是边长为4的正方形ABCD所在平面外一点,AP=2,且AP与平面ABCD成45°角,则CP的最小值为2
| 5 |
2
.| 5 |
分析:由于AP与平面ABCD成45°角,所以当平面PAC垂直于平面ABCD时,CP 最小,再利用余弦定理可求.
解答:解:根据题意,当平面PAC垂直于平面ABCD时,CP 最小
在△PAC中,PC2=22+32-2×2×4
×cos45°=20
∴CP=2
故答案为2
在△PAC中,PC2=22+32-2×2×4
| 2 |
∴CP=2
| 5 |
故答案为2
| 5 |
点评:本题以线面角为载体,考查线面垂直,考查余弦定理的运用,属于基础题.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
 B.
B.  C.
C.
 D.
D.

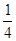 B.
B.
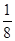 C.
C.
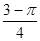 D.
D.