Question

15．在直角坐标系xOy中，已知点A（1，0），B（2，1），C（1，$\frac{3}{2}$），点P（x，y）在△ABC三边围成的区域（含边界）内，且$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{BC}$（m，n∈R）．
（1）若m=-2，n=2，求|$\overrightarrow{OP}$|；
（2）用x，y表示2m-$\frac{n}{2}$，并求2m-$\frac{n}{2}$的取值范围．

Answer 1

分析 （1）根据平面向量的坐标运算，求出向量$\overrightarrow{OP}$以及模长|$\overrightarrow{OP}$|；
（2）利用平面向量的坐标运算，用x、y表示出2m-$\frac{1}{2}$n，利用线性规划求出它的最值即可．

解答 解：（1）∵点A（1，0），B（2，1），C（1，$\frac{3}{2}$），
∴$\overrightarrow{AB}$=（1，1），$\overrightarrow{BC}$=（-1，$\frac{1}{2}$）；
∴当m=-2，n=2时，
$\overrightarrow{OP}$=-2$\overrightarrow{AB}$+2$\overrightarrow{BC}$
=-2（1，1）+2（-1，$\frac{1}{2}$）
=（-2-2，-2+1）
=（-4，-1）；
∴|$\overrightarrow{OP}$|=$\sqrt{{（-4）}^{2}{+（-1）}^{2}}$=$\sqrt{17}$；
（2）∵$\overrightarrow{OP}$=m$\overrightarrow{AB}$+n$\overrightarrow{BC}$
=m（1，1）+n（-1，$\frac{1}{2}$）
=（m-n，m+$\frac{1}{2}$n），
设$\overrightarrow{OP}$=（x，y），则$\left\{\begin{array}{l}{x=m-n}\\{y=m+\frac{1}{2}n}\end{array}\right.$，
∴两式相加得，2m-$\frac{1}{2}$n=x+y；
令x+y=t，y=-x+t
由图可知，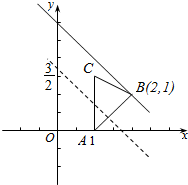

当直线y=-x+t过点B（2，1）时，t取得最大值是2+1=3，
当直线y=-x+t过点A（1，0）时，t取得最小值是1+0=1，
∴2m-$\frac{n}{2}$的取值范围是[1，3]．

点评 本题考查了平面向量的坐标运算问题，也考查了线性规划的应用问题，是综合性题目．