题目内容
(2014·大连模拟)已知f(x)=alnx+
x2,若对任意两个不等的正实数x1,x2都有
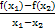>0成立,则实数a的取值范围是( )
x2,若对任意两个不等的正实数x1,x2都有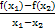>0成立,则实数a的取值范围是( )| A．[0,+∞) | B．(0,+∞) |
| C．(0,1) | D．(0,1] |
A
因为f(x)=alnx+
x2,
所以f′(x)=
+x.
又对?x1,x2∈(0,+∞),x1≠x2,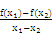
>0恒成立,
即f(x1)-f(x2)与x1-x2同号,
得f(x)在(0,+∞)上为增函数,
所以f′(x)=+x≥0在(0,+∞)上恒成立,
即a≥-x2在(0,+∞)上恒成立,
所以a≥0.
x2,所以f′(x)=
+x.又对?x1,x2∈(0,+∞),x1≠x2,
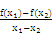>0恒成立,即f(x1)-f(x2)与x1-x2同号,
得f(x)在(0,+∞)上为增函数,
所以f′(x)=
+x≥0在(0,+∞)上恒成立,即a≥-x2在(0,+∞)上恒成立,
所以a≥0.
练习册系列答案
高中必刷题系列答案
相关题目
＋
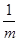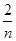的最小值为________．
，两边求导数得
＝
，于是y′＝f(x)g(x)·
的一个单调递增区间为( )．
＜1，则实数a的取值范围是________；
(x2－2ax＋3)在(－∞，1]内为增函数，则实数a的取值范围是________．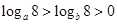
，那么a、b间的关系是()
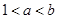
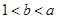
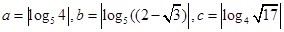,则( )
