题目内容
(1)(本小题满分7分)选修4-2:矩阵与变换
已知矩阵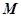
 ,其中
,其中 ,若点
,若点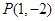 在矩阵
在矩阵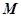 的变换下得到点
的变换下得到点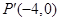 ,
,
(Ⅰ)求实数a的值; (Ⅱ)求矩阵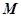 的特征值及其对应的特征向量.
的特征值及其对应的特征向量.
(2)(本小题满分7分)选修4-4:坐标系与参数方程
已知直线的极坐标方程为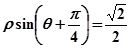 ,圆
,圆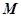 的参数方程为
的参数方程为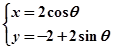
(其中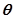 为参数).
为参数).
(Ⅰ)将直线的极坐标方程化为直角坐标方程;
(Ⅱ)求圆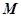 上的点到直线的距离的最小值.
上的点到直线的距离的最小值.
【答案】
(1)选修4-2:矩阵与变换
解:(1)解:(Ⅰ)由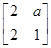
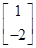 =
= , ∴
, ∴ .
-------------------3分
.
-------------------3分
(Ⅱ)由(Ⅰ)知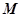
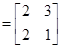 ,则矩阵
,则矩阵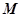 的特征多项式为
的特征多项式为
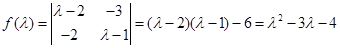 --------------------------5分
--------------------------5分
令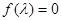 ,得矩阵
,得矩阵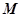 的特征值为
的特征值为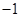 与4. (5分)
与4. (5分)
当 时,
时, 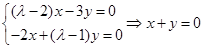
∴矩阵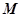 的属于特征值
的属于特征值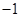 的一个特征向量为
的一个特征向量为 ;
---------------------------------6分
;
---------------------------------6分
当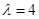 时,
时, 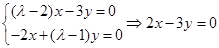
∴矩阵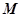 的属于特征值
的属于特征值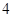 的一个特征向量为
的一个特征向量为 .
------------------------------7分
.
------------------------------7分
(2)选修4-4:坐标系与参数方程
(Ⅰ)以极点为原点,极轴为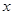 轴正半轴建立直角坐标系. ----------------1分
轴正半轴建立直角坐标系. ----------------1分
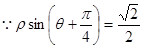
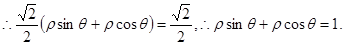 ----------------2分
----------------2分
所以,该直线的直角坐标方程为: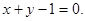 ----------------3分
----------------3分
(Ⅱ)圆 的普通方程为:
的普通方程为: ----------------4分
----------------4分
圆心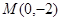 到直线
到直线 的距离
的距离 ---------------5分
---------------5分
所以,圆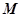 上的点到直线的距离的最小值为
上的点到直线的距离的最小值为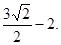 ----------------7分
----------------7分
【解析】略

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案
相关题目
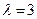 及对应的一个特征向量
及对应的一个特征向量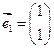 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点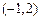 变换成
变换成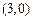 ,求矩阵M。
,求矩阵M。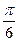 的直线
的直线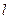 与圆C:
与圆C: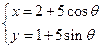 (
(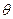 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定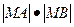 的值。
的值。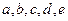 满足
满足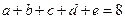 ,
,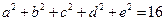 ,试确定
,试确定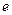 的最大值。
的最大值。 ,N=
,N= ,且MN=
,且MN= 。
。 =2
=2 sin
sin 。
。 3的解集为
3的解集为 ,求实数a的值;
,求实数a的值; 中,把矩阵
中,把矩阵 确定的压缩变换
确定的压缩变换 与矩阵
与矩阵 确定的旋转变换
确定的旋转变换 进行复合,得到复合变换
进行复合,得到复合变换 .
.
 在复合变换
在复合变换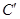 的方程.
的方程. 的参数方程为
的参数方程为 (
( 为参数),
为参数), 、
、 分别为直线
分别为直线 轴、
轴、 轴的交点,线段
轴的交点,线段 的中点为
的中点为 .
. 为极点,
为极点, 的极坐标方程.
的极坐标方程. 的解集与关于
的解集与关于 的解集相等.
的解集相等. ,
, 的值;
的值;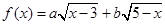 的最大值,以及取得最大值时
的最大值,以及取得最大值时 及对应的一个特征向量
及对应的一个特征向量 ,并且矩阵M对应的变换将点
,并且矩阵M对应的变换将点 变换成
变换成 ,求矩阵M。
,求矩阵M。 的直线
的直线 与圆C:
与圆C: (
( 为参数)相交于A、B两点,试确定
为参数)相交于A、B两点,试确定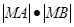 的值。
的值。 满足
满足 ,
, ,试确定
,试确定 的最大值。
的最大值。