题目内容
已知函数f(x)=sinωx+
cosωx(ω>0)的周期为π.
(1)求函数f(x)的振幅,初相;
(2)用五点法作出在长度为一个周期的闭区间上的图象;
(3)说明函数f(x)的图象可由y=sinx的图象经过怎样的变换而得到的?
| 3 |
(1)求函数f(x)的振幅,初相;
(2)用五点法作出在长度为一个周期的闭区间上的图象;
(3)说明函数f(x)的图象可由y=sinx的图象经过怎样的变换而得到的?
考点:由y=Asin(ωx+φ)的部分图象确定其解析式,两角和与差的正弦函数,函数y=Asin(ωx+φ)的图象变换
专题:三角函数的图像与性质
分析:(1)利用两角和的正弦公式求得f(x)=2sin(ωx+
)(ω>0),再根据它的周期为
=π,求得ω的值,可得f(x)=2sin(ωx+
),从而求得振幅和初相.
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
(3)根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
| π |
| 3 |
| 2π |
| ω |
| π |
| 3 |
(2)用五点法作函数y=Asin(ωx+φ)在一个周期上的简图.
(3)根据函数y=Asin(ωx+φ)的图象变换规律,可得结论.
解答:
解:(1)∵函数f(x)=sinωx+
cosωx=2sin(ωx+
)(ω>0)的周期为T=
=π,
∴ω=2,f(x)=2sin(2x+
),∴振幅为2,初相为
.
(2)列表:
作图:
(3)由y=sinx的图象向左平移
个单位,再把所得图象上的各点的横坐标变为原来的
,再把所得图象上的各点的纵坐标变为原来的2倍,即可得到函数f(x)的图象.
| 3 |
| π |
| 3 |
| 2π |
| ω |
∴ω=2,f(x)=2sin(2x+
| π |
| 3 |
| π |
| 3 |
(2)列表:
2x+
|
0 |
|
π |
|
2π | ||||||||||
| x | -
|
|
|
|
| ||||||||||
| f(x) | 0 | 2 | 0 | -2 | 0 |

(3)由y=sinx的图象向左平移
| π |
| 3 |
| 1 |
| 2 |
点评:本题主要考查函数y=Asin(ωx+φ)的图象性质,用五点法作函数y=Asin(ωx+φ)在一个周期上的简图,函数y=Asin(ωx+φ)的图象变换规律,属于基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知f(x)=x3-px2-qx和图象与x轴切于(1,0),则f(x)的极值情况是( )
A、极大值为f(
| ||
B、极大值为f(1),极小值为f(
| ||
C、极大值为f(
| ||
| D、极小值为f(1),没有极大值 |
下列函数中,以π为周期的偶函数是( )
| A、y=sin|x| | ||
| B、y=|cosx| | ||
C、y=cos(2x-
| ||
D、y=sin(x+
|
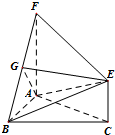 如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF
如图,三角形ABC和梯形ACEF所在的平面互相垂直,AB⊥BC,AF⊥AC,AF