题目内容
抛物线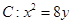 与直线
与直线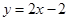 相交于
相交于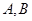 两点,点
两点,点 是抛物线
是抛物线 上不同
上不同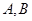 的一点,若直线
的一点,若直线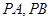 分别与直线
分别与直线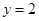 相交于点
相交于点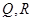 ,
,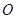 为坐标原点,则
为坐标原点,则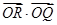 的值是( )
的值是( )
| A.20 | B.16 | C.12 | D.与点 位置有关的一个实数 位置有关的一个实数 |
A
解析试题分析:由抛物线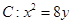 与直线
与直线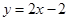 联立方程得
联立方程得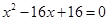 ,设
,设 .所以
.所以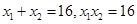 .所以直线PA:
.所以直线PA: 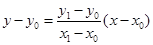 .令y=2.
.令y=2.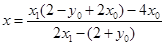 .即
.即 .同理
.同理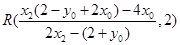 .所以
.所以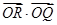
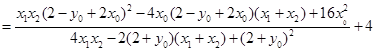
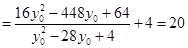 .故选A.
.故选A.
考点:1.直线与圆锥曲线的关系.2.向量的数量积.3.方程的思想.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知 ,
, ,则
,则 与
与 的夹角为( )
的夹角为( )
A. | B. | C. | D. |
若A ,B
,B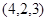 ,C
,C ,则△ABC的形状是( )
,则△ABC的形状是( )
| A.锐角三角形 | B.直角三角形 |
| C.钝角三角形 | D.等腰三角形 |
平面向量 满足
满足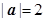 ,
,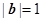 ,且
,且 的夹角为
的夹角为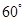 ,则
,则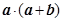 = ( )
= ( )
| A.1 | B.3 | C.5 | D.7 |
设 、
、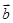 是两个非零向量,则使
是两个非零向量,则使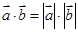 成立的一个必要非充分的条件是( )
成立的一个必要非充分的条件是( )
A.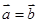 | B.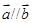 | C.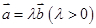 | D.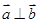 |
已知A,B,C三点的坐标分别是A(3,0),B(0,3),C(cos α,sin α),α∈ ,若
,若 =-1,则
=-1,则 的值为( )
的值为( )
A.- | B.- | C.2 | D.3 |
在空间中,已知 =(2,4,0),
=(2,4,0), =(-1,3,0),则∠ABC的大小为( )
=(-1,3,0),则∠ABC的大小为( )
| A.45° | B.90° | C.120° | D.135° |
已知△ABC中, =a,
=a, =b,a·b<0,
=b,a·b<0, ,|a|=3,|b|=5,
,|a|=3,|b|=5,
则a与b的夹角是( )
| A.30° |
| B.150° |
| C.210° |
| D.30°或150° |
 β=
β= .若平面向量
.若平面向量 ,
, 满足
满足 ,
, ∈(0,
∈(0, ),且
),且 和
和 都在集合{
都在集合{ |n∈Z}中,则
|n∈Z}中,则 ( )
( )

