Question

（本小题满分10分）

 在平面直角坐标系xOy中，已知点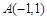，P是动点，且三角形POA的三边所在直线的斜

率满足k_OP+k_OA=k_PA．

 (1)求点P的轨迹C的方程；

(2)若Q是轨迹C上异于点P的一个点，且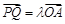，直线OP与QA交于点M，问：是否存在点P使得△PQA和△PAM的面积满足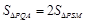?若存在，求出点P的坐标；若不存在，说明理由．

 

 

Answer 1

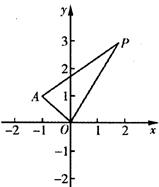
【答案】

解：（1）设点为所求轨迹上的任意一点，则由得，

，整理得轨迹的方程为（且）.······· 3分

（2）:学设

由可知直线，则，

故，即，      …………5分

直线OP方程为：   ①；

直线QA的斜率为：，

∴直线QA方程为：，

即  ②           

联立①②，得，∴点M的横坐标为定值．       …………8分

由，得到，因为，所以，

由，得，∴的坐标为．

∴存在点P满足，的坐标为．······················ 10分

 

【解析】略