题目内容
已知x满足不等式(log2x)2-log2x2≤0,求函数y=4x-| 1 |
| 2 |
| a2 |
| 2 |
分析:根据指数的运算性质,我们可将函数y=4x-
-a•2x+
+1(a∈R)的解析式化为y=
(2x-a)2+1,由x满足不等式(log2x)2-log2x2≤0,我们求出满足条件的x的取值范围,结合二次函数在定区间了最小值的确定方法,我们易求出函数y=4x-
-a•2x+
+1(a∈R)的最小值.
| 1 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
解答:解:解不等式 (log2x)2-log2x2≤0,
得 1≤x≤4,
所以 2≤2x≤16
y=4x-
-a•2x+
+1=
(2x)2-a•2x+
+1=
(2x-a)2+1
当a<2时,ymin=
(2-a)2+1;
当2≤a≤16时,ymin=1
当a>16时,ymin=
(16-a)2+1
得 1≤x≤4,
所以 2≤2x≤16
y=4x-
| 1 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
| a2 |
| 2 |
| 1 |
| 2 |
当a<2时,ymin=
| 1 |
| 2 |
当2≤a≤16时,ymin=1
当a>16时,ymin=
| 1 |
| 2 |
点评:本题考查的知识点是对数函数的图象与性质,指数的运算性质,二次函数在定区间上的最值问题,其中根据已知求出满足条件的x的取值范围,进而求出2x的取值范围,将问题转化为二次函数在定区间上的最值问题,是解答本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) B、
B、
 D、m,n的关系不能确定
D、m,n的关系不能确定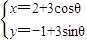 (θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .
(θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .