题目内容
已知函数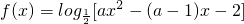 的值域为R,且f(x)在(2,5)上是减函数,则实数a的取值范围是
的值域为R,且f(x)在(2,5)上是减函数,则实数a的取值范围是
- A.a>0
- B.a≥0
- C.0≤a≤2
- D.
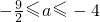
A
分析:函数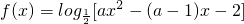 的值域为R等价于ax2-(a-1)x-2能取遍一切正实数,即△=a2-2a+1+8a≥0,解之
的值域为R等价于ax2-(a-1)x-2能取遍一切正实数,即△=a2-2a+1+8a≥0,解之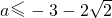 或
或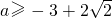 .再由f(x)在(2,5)上是减函数,根据复合函数的单调性可知
.再由f(x)在(2,5)上是减函数,根据复合函数的单调性可知 ,解得a>0.取这两种情况的交集得实数a的取值范围.
,解得a>0.取这两种情况的交集得实数a的取值范围.
解答:∵函数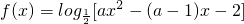 的值域为R,∴ax2-(a-1)x-2能取遍一切正实数,∴△=a2-2a+1+8a≥0,解之
的值域为R,∴ax2-(a-1)x-2能取遍一切正实数,∴△=a2-2a+1+8a≥0,解之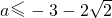 或
或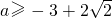 .∵f(x)在(2,5)上是减函数,∴根据复合函数的单调性可知
.∵f(x)在(2,5)上是减函数,∴根据复合函数的单调性可知 ,解之a>0.{a|
,解之a>0.{a|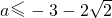 或
或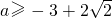 }∩{a|a>0}={a|a≥-3+2
}∩{a|a>0}={a|a≥-3+2 },∴实数a的取值范围是
},∴实数a的取值范围是 .故上述四个选项均不对.正确答案是:实数a的取值范围是
.故上述四个选项均不对.正确答案是:实数a的取值范围是
点评:解这类问题一是要注意对数函数的值域为R时真数的取值范围是全体正实数,二是要注意复合函数的单调性:同增异减.
分析:函数
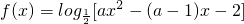 的值域为R等价于ax2-(a-1)x-2能取遍一切正实数,即△=a2-2a+1+8a≥0,解之
的值域为R等价于ax2-(a-1)x-2能取遍一切正实数,即△=a2-2a+1+8a≥0,解之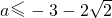 或
或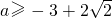 .再由f(x)在(2,5)上是减函数,根据复合函数的单调性可知
.再由f(x)在(2,5)上是减函数,根据复合函数的单调性可知 ,解得a>0.取这两种情况的交集得实数a的取值范围.
,解得a>0.取这两种情况的交集得实数a的取值范围.解答:∵函数
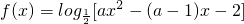 的值域为R,∴ax2-(a-1)x-2能取遍一切正实数,∴△=a2-2a+1+8a≥0,解之
的值域为R,∴ax2-(a-1)x-2能取遍一切正实数,∴△=a2-2a+1+8a≥0,解之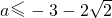 或
或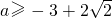 .∵f(x)在(2,5)上是减函数,∴根据复合函数的单调性可知
.∵f(x)在(2,5)上是减函数,∴根据复合函数的单调性可知 ,解之a>0.{a|
,解之a>0.{a|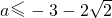 或
或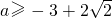 }∩{a|a>0}={a|a≥-3+2
}∩{a|a>0}={a|a≥-3+2 },∴实数a的取值范围是
},∴实数a的取值范围是 .故上述四个选项均不对.正确答案是:实数a的取值范围是
.故上述四个选项均不对.正确答案是:实数a的取值范围是
点评:解这类问题一是要注意对数函数的值域为R时真数的取值范围是全体正实数,二是要注意复合函数的单调性:同增异减.

练习册系列答案
相关题目
 的值域为R,则实数k的取值范围是__________
的值域为R,则实数k的取值范围是__________ 的值域为R,则实数a的取值范围是 .
的值域为R,则实数a的取值范围是 . 的值域为R,则m的取值范围为( )
的值域为R,则m的取值范围为( ) 的值域为R,则m的取值范围是( )
的值域为R,则m的取值范围是( )