题目内容
(满分12分) 偶函数f(x)的定义域为R,若f(x-1)=f(x+1)对一切x∈R恒成立,又当0≤x≤1时,f(x)=-x2+4.
(1)求证f(x)是周期函数,并确定它的周期; (2)求当 1≤x≤2时,f(x)的解析式。
(满分12分)(1)∵ f(x)定义域为R且f(x-1)=f(x+1),
∴ f(x+2)=f(x+1+1)=f(x+1-1)=f(x),
则f(x)的一个周期为2,且2n(n∈Z,n≠0)都是y=f(x)的周期。
(2)设1≤x≤2,则-2≤-x≤-1,因此,0≤2-x≤1,
由已知有:f(2-x)=-(2-x)2+4,
∵ f(x)的周期为2,且为偶函数,∴ f(2-x)=f(-x)=f(x).
∴ 当1≤x≤2时,f(x)=-(2-x)2+4。

练习册系列答案
 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案
相关题目
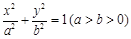 的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知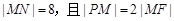 .
.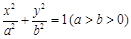 的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知
的左焦点,直线l为其左准线,直线l与x轴交于点P,线段MN为椭圆的长轴,已知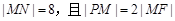 .
.