题目内容
在三棱锥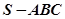 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 平面
平面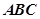 ,
,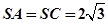 ,
,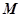 、
、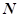 分别为
分别为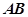 、
、 的中点,
的中点,
(1)证明: ;
;
(2)求二面角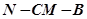 的大小;
的大小;
(3)求点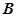 到平面
到平面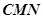 的距离.
的距离.
【答案】
arctan2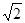 ,
,
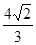
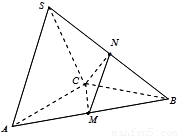
【解析】.解:(Ⅰ)取AC中点D,连结SD、DB.
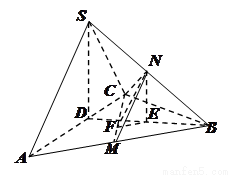 ∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD, ∴AC⊥平面SDB,又SB
∵SA=SC,AB=BC,∴AC⊥SD且AC⊥BD, ∴AC⊥平面SDB,又SB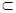 平面SDB,
平面SDB,
∴AC⊥SB.
(Ⅱ)∵AC⊥平面SDB,AC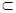 平面ABC,∴平面SDB⊥平面ABC.
平面ABC,∴平面SDB⊥平面ABC.
过N作NE⊥BD于E,NE⊥平面ABC,
过E作EF⊥CM于F,连结NF,
则NF⊥CM.
∴∠NFE为二面角N-CM-B的平面角.
∵平面SAC⊥平面ABC,SD⊥AC,∴SD⊥平面ABC.
又∵NE⊥平面ABC,∴NE∥SD.
∵SN=NB,∴NE=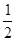 SD=
SD=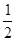
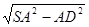 =
=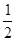
 =
=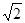 ,且ED=EB.
,且ED=EB.
在正△ABC中,由平几知识可求得EF=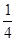 MB=
MB=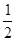 ,在Rt△NEF中,tan∠NFE=
,在Rt△NEF中,tan∠NFE=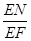 =2
=2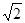 ,∴二面角N—CM—B的大小是arctan2
,∴二面角N—CM—B的大小是arctan2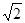
(Ⅲ)在Rt△NEF中,NF=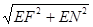 =
=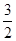 ,
,
∴S△CMN=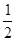 CM·NF=
CM·NF=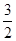
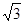 ,S△CMB=
,S△CMB=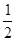 BM·CM=2
BM·CM=2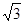 .
.
设点B到平面CMN的距离为h,
∵VB-CMN=VN-CMB,NE⊥平面CMB,∴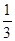 S△CMN·h=
S△CMN·h=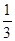 S△CMB·NE,
S△CMB·NE,
∴h=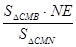 =
=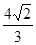 .即点B到平面CMN的距离为
.即点B到平面CMN的距离为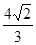

练习册系列答案
相关题目
 中,
中,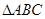 是边长为
是边长为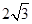 的正三角形,平面
的正三角形,平面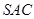 ⊥平面
⊥平面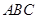 ,
,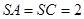 ,
,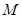 、
、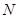 分别为
分别为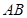 、
、 的中点.
的中点.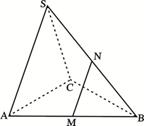
 ⊥
⊥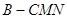 的体积.
的体积. 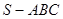 中,
中,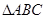 是边长为4的正三角形,
是边长为4的正三角形,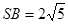 ,
, ,
,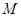 、
、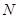 分别是
分别是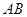 、
、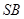 的中点;
的中点;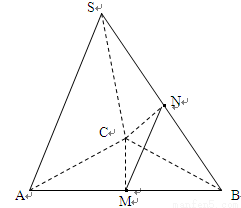
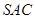
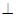 平面
平面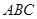 ;
;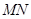 与平面
与平面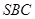 所成角的正弦值。
所成角的正弦值。 中,
中,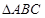 是边长为
是边长为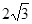 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
,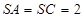 ,
, 、
、 分别为
分别为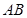 、
、 的中点。
的中点。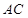 ⊥
⊥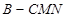 的体积.
的体积.
 中,
中, 是边长为
是边长为 的正三角形,平面
的正三角形,平面 ⊥平面
⊥平面 ,
, ,
, 、
、 分别为
分别为 、
、 的中点。
的中点。 ⊥
⊥ 的体积.
的体积.