题目内容
已知点A(1、1),曲线C上的点(x、y)满足:
,一束光线从点A出发经y轴反射到曲线C上的最短路程是( )
|
A、6
| ||
B、5
| ||
| C、8 | ||
| D、10 |
分析:把圆的参数方程化为普通方程后,找出圆心B的坐标和半径r,然后根据题意画出图形,找出A关于y轴的对称点A′的坐标,连接A′B,根据平面镜的反射法则得到A′C即为光线从点A出发经y轴反射到曲线C上的最短路程,利用两点间的距离公式,由点A′和圆心B的坐标,求出|A′B|,然后减去圆的半径即可得到|A′C|的值.
解答: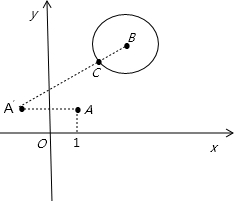 解:把曲线C的参数方程化为普通方程得:(x-5)2+(y-7)2=4,
解:把曲线C的参数方程化为普通方程得:(x-5)2+(y-7)2=4,
所以曲线C为圆心B的坐标(5,7),半径r=2的圆,
所以把y轴看作一面镜子,找出A关于y轴的对称点A′的坐标为(-1,1),
连接A′B,与圆交于C点,则|A′C|为光线反射到圆上的最短距离,
因为|A′B|=
=6
,且r=|BC|=2,
所以|A′C|=|A′B|-|BC|=6
-2.
故选A
 解:把曲线C的参数方程化为普通方程得:(x-5)2+(y-7)2=4,
解:把曲线C的参数方程化为普通方程得:(x-5)2+(y-7)2=4,所以曲线C为圆心B的坐标(5,7),半径r=2的圆,
所以把y轴看作一面镜子,找出A关于y轴的对称点A′的坐标为(-1,1),
连接A′B,与圆交于C点,则|A′C|为光线反射到圆上的最短距离,
因为|A′B|=
| (5+1)2+(7-1)2 |
| 2 |
所以|A′C|=|A′B|-|BC|=6
| 2 |
故选A
点评:此题考查学生灵活运用两点间的距离公式化简求值,考查了数形结合的数学思想,是一道中档题.此题的关键是找出反射光线的最短距离.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 在平面直角坐标系xoy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA
在平面直角坐标系xoy中,已知点A(-1,1),P是动点,且△POA的三边所在直线的斜率满足kOP+kOA=kPA