题目内容
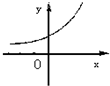
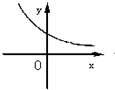
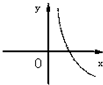
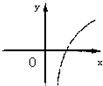
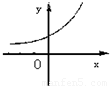
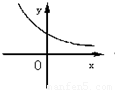
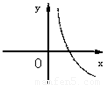
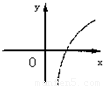
设0<a<1,实数x,y满足x+logay=0,则y关于x的函数的图象大致形状是 ( )
A.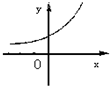 | B.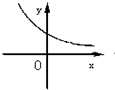 | C.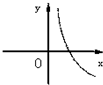 | D.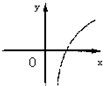 |
∵x+logay=0
∴logay=-x
∴y=a-x,即y=(a-1)x=(
)x
又∵0<a<1
∴
>1
∴指数函数y=(
)x的图象单调递增,过点(0,1)
故选A
∴logay=-x
∴y=a-x,即y=(a-1)x=(
| 1 |
| a |
又∵0<a<1
∴
| 1 |
| a |
∴指数函数y=(
| 1 |
| a |
故选A

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
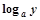 =0,则y关于x的函数的图象大致形状是( )
=0,则y关于x的函数的图象大致形状是( )