题目内容
【题目】如图，在四棱锥P﹣ABCD中，底面ABCD为平行四边形，AP=AB=AC=a， 
，PA⊥底面ABCD． 
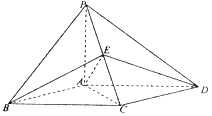
（1）求证：平面PCD⊥平面PAC；
（2）在棱PC上是否存在一点E，使得二面角B﹣AE﹣D的平面角的余弦值为 
？若存在，求出 
的值？若不存在，说明理由．
【答案】
（1）证明：在△ACD中，AC=a，CD=a，AD= 
a，
由勾股定理得：CD⊥AC
∵PA⊥底面ABCD，∴PA⊥CD，
AC面PAC，PA面PAC，PA∩AC=A
∴CD⊥面PAC
又∵CD面PCD
∴平面PCD⊥平面PAC
（2）解：（由（1）知：AB⊥AC，又PA⊥底面ABCD
∴以A为原点，AB，AC，AP所在直线分别为x轴，y轴，z轴建立如图所示坐标系
则A（0，0，0），B（a，0，0），C（0，a，0），
D（﹣a，a，0），P（0，0，a）
假设点E存在，且λ= 
，则 
=λ 
（xE，yE﹣a，zE）=λ（0，﹣a，a）
∴xE=0，yE=（1﹣λ）a，zE=λa
=（a，0，0） 
=（0，（1﹣λ）a，λa）， 
=（﹣a，a，0）
设平面BAE的法向量为 
=（x1，y1，z1），平面DAE的法向量为 
=（x2，y2，z2），
则 
，取y1=λ，得 
，
，取x2=λ，得 =（λ，λ，λ﹣1）
cos＜ 
＞= 
= 
= 
，
由题意：|cos＜ ＞|= = 
，
整理得：3（2λ2﹣2λ+1）=2（3λ2﹣2λ+1），解得λ= 
，
∴棱PC上存在一点E，使得二面角B﹣AE﹣D的平面角的余弦值为﹣ ，且此时λ= 
．
【解析】（1）由勾股定理得：CD⊥AC，由线面垂直得PA⊥CD，从而CD⊥面PAC，由此能证明平面PCD⊥平面PAC．（2）以A为原点，AB，AC，AP所在直线分别为x轴，y轴，z轴建立空间直角坐标系，利用向量法能求出结果．
【考点精析】利用平面与平面垂直的判定对题目进行判断即可得到答案，需要熟知一个平面过另一个平面的垂线，则这两个平面垂直．
