题目内容
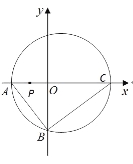
【题目】在平面直角坐标系xOy中，矩形ABCD的一边AB在x轴上，另一边CD在x轴上方，且AB＝8，BC＝6，其中A（－4，0）、B（4，0）
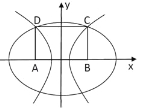
（1）若A、B为椭圆的焦点，且椭圆经过C、D两点，求该椭圆的方程；
（2）若A、B为双曲线的焦点，且双曲线经过C、D两点，求双曲线的方程；
【答案】（1）
（2）
【解析】
试题分析：（1）由椭圆的定义：丨CA丨+丨CB丨=16=2a，求得a=8，则
=64-16=48，即可求得椭圆方程；（2）根据双曲线的定义：丨CA丨-丨CB丨=4=2a′，则求得a′=2，则
=16-4=12，即可求得双曲线的标准方程
试题解析：由题意：
, AC=10……………2分
（1）∵A、B为椭圆的焦点，且椭圆经过C、D两点
根据椭圆的定义：
∴ 
…………4分
在椭圆中：
…………6分
∴所求椭圆方程为： …………8分
（2）∵A、B为双曲线的焦点，且双曲线经过C、D两点
根据双曲线的定义：
∴ 
…………10分
在双曲线中：
…………12分
∴所求双曲线方程为： …………14分
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
