题目内容
已知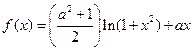

 .
.
(1)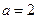 时,求
时,求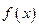 的极值
的极值
(2)当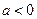 时,讨论
时,讨论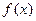 的单调性。
的单调性。
(3)证明: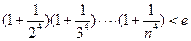 (
(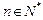 ,
,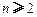 ,其中无理数
,其中无理数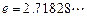 )
)
解:
(1)令 ,知
,知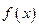 在区间
在区间 上单调递
上单调递 增
增
 ,
, 上
上
单调递减,在 单调递增。
单调递增。
故有极大值 ,极小值
,极小值 。
。
(2)当 时,
时, 上单调递减,
上单调递减, 单调递增,
单调递增, 单调递减
单调递减
当 时,
时, 单调递减
单调递减
当 时,
时, 上单调递减,
上单调递减, 单调递增,
单调递增, 单调递减
单调递减
(3)由(Ⅰ)当 时,
时, 在
在 上单调递减。
上单调递减。
当 时
时
∴
 ,即
,即

解析

练习册系列答案
相关题目
题目内容
已知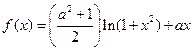

 .
.
(1)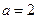 时,求
时,求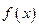 的极值
的极值
(2)当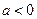 时,讨论
时,讨论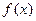 的单调性。
的单调性。
(3)证明: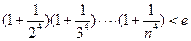 (
(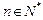 ,
,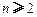 ,其中无理数
,其中无理数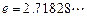 )
)
解:
(1)令 ,知
,知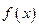 在区间
在区间 上单调递
上单调递 增
增
 ,
, 上
上
单调递减,在 单调递增。
单调递增。
故有极大值 ,极小值
,极小值 。
。
(2)当 时,
时, 上单调递减,
上单调递减, 单调递增,
单调递增, 单调递减
单调递减
当 时,
时, 单调递减
单调递减
当 时,
时, 上单调递减,
上单调递减, 单调递增,
单调递增, 单调递减
单调递减
(3)由(Ⅰ)当 时,
时, 在
在 上单调递减。
上单调递减。
当 时
时
∴
 ,即
,即

解析
