题目内容
已知正项数列{an}满足 ,
,
(1)求数列的通项an;
(2)求证: .
.
解:由已知 可得,
可得, ,
,
即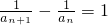
数列{ }是以
}是以 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列
∴ 即
即
∵0<P<1∴
∴

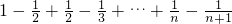 =
= 即证
即证
分析:(1)由已知 可得,
可得, ,
, 即
即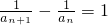
数列{ }是以
}是以 为首项,以1为公差的等差数列,从而可求
为首项,以1为公差的等差数列,从而可求
(2)由(1)可得 结合0<P<1可得
结合0<P<1可得 ,利用裂项求和可证
,利用裂项求和可证
点评:本题主要考查了利用构造等差数列求解通项公式、裂项求和是证明(2)的关键,解题的难点在于发现通项中 .
.
 可得,
可得, ,
,
即
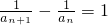
数列{
 }是以
}是以 为首项,以1为公差的等差数列
为首项,以1为公差的等差数列∴
 即
即
∵0<P<1∴

∴


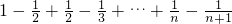 =
= 即证
即证分析:(1)由已知
 可得,
可得, ,
, 即
即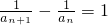
数列{
 }是以
}是以 为首项,以1为公差的等差数列,从而可求
为首项,以1为公差的等差数列,从而可求(2)由(1)可得
 结合0<P<1可得
结合0<P<1可得 ,利用裂项求和可证
,利用裂项求和可证点评:本题主要考查了利用构造等差数列求解通项公式、裂项求和是证明(2)的关键,解题的难点在于发现通项中
 .
. 
练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目