题目内容
已知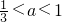 ,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a).
,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a).
(1)求g(a)的解析表达式;
(2)若对一切 都有kg(a)-1<0成立,求实数k的取值范围.
都有kg(a)-1<0成立,求实数k的取值范围.
解:(1)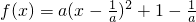 x∈[1,3]
x∈[1,3]
由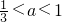 知,
知, .从而
.从而
∴当 即
即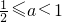 时,M(a)=f(3)=9a-5
时,M(a)=f(3)=9a-5
当 即
即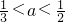 时,M(a)=f(1)=a-1
时,M(a)=f(1)=a-1
∴
(2)当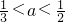 时,
时,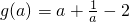 为减函数.
为减函数.
∴ .
.
要使kg(a)-1<0恒成立,则 恒成立.而
恒成立.而
∴ .
.
又当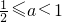 时,
时, 为增函数
为增函数
∴
要使kg(a)-1<0恒成立.则 恒成立.而
恒成立.而
∴
综上得, .
.
分析:(1)将f(x)=ax2-2x+1配方化为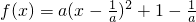 ,由
,由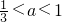 可求
可求 ,求得N(a);根据f(x)的对称轴
,求得N(a);根据f(x)的对称轴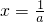 在区间[1,3]的位置情况分类讨论,求得M(a),从而求得g(a)的解析表达式;
在区间[1,3]的位置情况分类讨论,求得M(a),从而求得g(a)的解析表达式;
(2)对 ,分段研究函数的单调性,从而可求得各段上g(a)及
,分段研究函数的单调性,从而可求得各段上g(a)及 的取值范围,及k满足的关系式,再利用“小小取小”的恒成立思想即可解决问题.
的取值范围,及k满足的关系式,再利用“小小取小”的恒成立思想即可解决问题.
点评:本题考查二次函数在闭区间上的最值,着重考查学生分类讨论思想与转化思想及恒成立思想的应用,中档题.
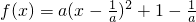 x∈[1,3]
x∈[1,3]由
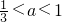 知,
知, .从而
.从而
∴当
 即
即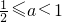 时,M(a)=f(3)=9a-5
时,M(a)=f(3)=9a-5当
 即
即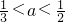 时,M(a)=f(1)=a-1
时,M(a)=f(1)=a-1∴

(2)当
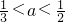 时,
时,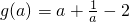 为减函数.
为减函数.∴
 .
.要使kg(a)-1<0恒成立,则
 恒成立.而
恒成立.而
∴
 .
.又当
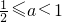 时,
时, 为增函数
为增函数∴

要使kg(a)-1<0恒成立.则
 恒成立.而
恒成立.而
∴

综上得,
 .
.分析:(1)将f(x)=ax2-2x+1配方化为
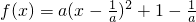 ,由
,由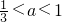 可求
可求 ,求得N(a);根据f(x)的对称轴
,求得N(a);根据f(x)的对称轴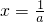 在区间[1,3]的位置情况分类讨论,求得M(a),从而求得g(a)的解析表达式;
在区间[1,3]的位置情况分类讨论,求得M(a),从而求得g(a)的解析表达式;(2)对
 ,分段研究函数的单调性,从而可求得各段上g(a)及
,分段研究函数的单调性,从而可求得各段上g(a)及 的取值范围,及k满足的关系式,再利用“小小取小”的恒成立思想即可解决问题.
的取值范围,及k满足的关系式,再利用“小小取小”的恒成立思想即可解决问题.点评:本题考查二次函数在闭区间上的最值,着重考查学生分类讨论思想与转化思想及恒成立思想的应用,中档题.

练习册系列答案
 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
 若f(x)>3,则x的取值范围是( )
若f(x)>3,则x的取值范围是( )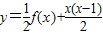 的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;
的反函数为p(x),t(x)=p(x)(1-x),求函数t(x)的最大值;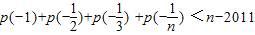 恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由.
恒成立?若存在,请找出一个满足条件的N的值,并给以说明;若不存在,请说明理由. ,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a).
,若f(x)=ax2-2x+1在区间[1,3]上的最大值为M(a),最小值为N(a),记g(a)=M(a)-N(a). 都有kg(a)-1<0成立,求实数k的取值范围.
都有kg(a)-1<0成立,求实数k的取值范围. 若f(x)>3,则x的取值范围是( )
若f(x)>3,则x的取值范围是( )