Question

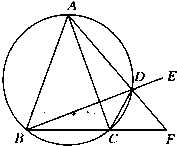
选修4-1：几何证明选讲
如图，圆O为△ABC的外接圆，且AB=AC，过点A的直线交圆O于点D，交BC的延长线于点F，DE是BD的延长线，连接CD．
（Ⅰ）求证：∠EDF=∠CDF；
（Ⅱ）求证：AB²=AF•AD．

Answer 1

分析：（1）由∠EDF=∠ADB，∠ADB=∠ACB，∠CDF=∠ABC，AB=AC，能够证明∠EDF=∠CDF．
（2）由∠ADC+∠ABC=180°，∠ACF+∠ACB=180°，知∠ADC=∠ACF，故△ADC≌△ACF，由此能够证明AB²=AD•AF．

解答：解：（1）∵∠EDF=∠ADB，
∠ADB=∠ACB，
∠CDF=∠ABC，AB=AC，
∴∠EDF=∠CDF；
（2）∵∠ADC+∠ABC=180°，
∠ACF+∠ACB=180°，
∴∠ADC=∠ACF，
∴△ADC∽△ACF，
∴

AC

AF

=

AD

AC

，
AC²=AD•AF，
∴AB²=AD•AF．

点评：本题考查与圆有关的比例线段的应用，是基础题．解题时要认真审题，仔细解答，注意合理地进行等价转化．