题目内容
已知：函数f（x）=2sin（x+
）（x∈[0，
]）的图象与直线y=m的三个交点的横坐标分别为x1，x2，x3（x1＜x2＜x3），那么x1+2x2+x3= ．
| π |
| 3 |
| 13π |
| 6 |
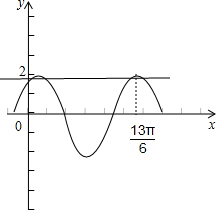
分析：作出函数，由图象平移的知识和三角函数的对称性可得x1+x2和x2+x3的值，相加即可．
解答：解：函数f（x）=2sin（x+
）（x∈[0，
]）的图象，
可看作函数y=2sinx的图象向左平移
得到，相应的对称轴也向左平移
，
∴x1+x2=2（
-
）=
，x2+x3=2（
-
）=
，
∴x1+2x2+x3=（x1+x2）+（x2+x3）=
故答案为：
| π |
| 3 |
| 13π |
| 6 |
可看作函数y=2sinx的图象向左平移
| π |
| 3 |
| π |
| 3 |
∴x1+x2=2（
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| 3π |
| 2 |
| π |
| 3 |
| 7π |
| 3 |
∴x1+2x2+x3=（x1+x2）+（x2+x3）=
| 8π |
| 3 |
故答案为：
| 8π |
| 3 |
点评：本题考查三角函数图象的变化和性质，利用对称性是解决问题的关键，属中档题．
练习册系列答案
出彩同步大试卷系列答案
相关题目