题目内容
已知函数f(x)=ln(1+x)-x+ax2,x∈[0,+∞),a∈R
 .
.
解:(1)当a= 时,f(x)=ln(1+x)-x+
时,f(x)=ln(1+x)-x+ x2,
x2,
∴f′(x)= =
=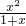 ≥0在x∈[0,+∞)恒成立,
≥0在x∈[0,+∞)恒成立,
∴f(x)在[0,+∞)上单调递增,
∴当x∈[0,+∞)时,f(x)≥f(0)=0,
故当x∈[0,+∞)时,f(x)≥0;
(2)∵f′(x)= =
= ,
,
①当 ,即a
,即a 时,f′(x)≥0在[0,+∞)上恒成立,∴f(x)≥f(0)=0;
时,f′(x)≥0在[0,+∞)上恒成立,∴f(x)≥f(0)=0;
②当 ,即a<0时,f′(x)≤0在[0,+∞)上恒成立,∴f(x)≤f(0)=0与题意不符;
,即a<0时,f′(x)≤0在[0,+∞)上恒成立,∴f(x)≤f(0)=0与题意不符;
③当 ,即0
,即0 时,f′(x)=
时,f′(x)= =
= ,
,
故在[0, )上,f′(x)≤0,
)上,f′(x)≤0,
∴f(x)≤f(0)=0与题意不符,
综上可得当且仅当a 时,f(x)≥0在[0,+∞)上恒成立.
时,f(x)≥0在[0,+∞)上恒成立.
分析:(1)把a= 代入已知式子,求导数可得函数单调增,进而可得f(x)≥f(0)=0;
代入已知式子,求导数可得函数单调增,进而可得f(x)≥f(0)=0;
(2)求导数可得f′(x)= ,分
,分 ,
, ,
, 三种情况讨论即可.
三种情况讨论即可.
点评:本题考查函数的单调性和导数的关系,以及恒成立问题,属中档题.
 时,f(x)=ln(1+x)-x+
时,f(x)=ln(1+x)-x+ x2,
x2,∴f′(x)=
 =
=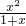 ≥0在x∈[0,+∞)恒成立,
≥0在x∈[0,+∞)恒成立,∴f(x)在[0,+∞)上单调递增,
∴当x∈[0,+∞)时,f(x)≥f(0)=0,
故当x∈[0,+∞)时,f(x)≥0;
(2)∵f′(x)=
 =
= ,
,①当
 ,即a
,即a 时,f′(x)≥0在[0,+∞)上恒成立,∴f(x)≥f(0)=0;
时,f′(x)≥0在[0,+∞)上恒成立,∴f(x)≥f(0)=0;②当
 ,即a<0时,f′(x)≤0在[0,+∞)上恒成立,∴f(x)≤f(0)=0与题意不符;
,即a<0时,f′(x)≤0在[0,+∞)上恒成立,∴f(x)≤f(0)=0与题意不符;③当
 ,即0
,即0 时,f′(x)=
时,f′(x)= =
= ,
,故在[0,
 )上,f′(x)≤0,
)上,f′(x)≤0,∴f(x)≤f(0)=0与题意不符,
综上可得当且仅当a
 时,f(x)≥0在[0,+∞)上恒成立.
时,f(x)≥0在[0,+∞)上恒成立.分析:(1)把a=
 代入已知式子,求导数可得函数单调增,进而可得f(x)≥f(0)=0;
代入已知式子,求导数可得函数单调增,进而可得f(x)≥f(0)=0;(2)求导数可得f′(x)=
 ,分
,分 ,
, ,
, 三种情况讨论即可.
三种情况讨论即可.点评:本题考查函数的单调性和导数的关系,以及恒成立问题,属中档题.

练习册系列答案
相关题目