题目内容
已知点A(0,1)、B(0,-1),P是一个动点,且直线PA、PB的斜率之积为 .
.
(1)求动点P的轨迹C的方程;
(2)设Q(2,0),过点(-1,0)的直线l交C于M、N两点,若对满足条件的任意直线l,不等式 恒成立,求λ的最小值.
恒成立,求λ的最小值.
解:(1)设动点P的坐标为(x,y),则直线PA,PB的斜率分别是 ,
,
由条件得 ,-----------------2分
,-----------------2分
即 动点P的轨迹C的方程为
动点P的轨迹C的方程为 -----------------6分分(注:无x≠0扣1分)
-----------------6分分(注:无x≠0扣1分)
(2)设点M,N的坐标分别是(x1,y1),(x2,y2),
ⅰ)当直线l垂直于x轴时,
∴
∴ ---------------10分
---------------10分
ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=k(x+1),
由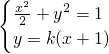 得(1+2k2)x2+4k2x+2k2-2=0----------11分
得(1+2k2)x2+4k2x+2k2-2=0----------11分
∴ ----------------12分
----------------12分
∴
又∵y1=k(x1+1),y2=k(x2+1),
∴ -----------------13分
-----------------13分
= -------------------14分
-------------------14分
综上所述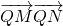 的最大值是
的最大值是 ----------------15分
----------------15分
∴λ的最小值为 -----------------------16分
-----------------------16分
分析:(1)设动点P的坐标为(x,y),可表示出直线PA,PB的斜率,根据题意直线PA、PB的斜率之积为 建立等式求得x和y的关系式,即点P的轨迹方程.
建立等式求得x和y的关系式,即点P的轨迹方程.
(2)设点M,N的坐标,当直线l垂直于x轴时,分别表示出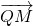 和
和  ,进而可求得
,进而可求得 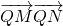 ;再看直线l不垂直于x轴时,设直线l的方程,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而表示出
;再看直线l不垂直于x轴时,设直线l的方程,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而表示出 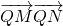 判断出其范围,综合求得
判断出其范围,综合求得 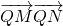 的最大值,根据
的最大值,根据 恒成立,求得λ的最小值.
恒成立,求得λ的最小值.
点评:本题主要考查了直线与圆锥曲线的综合问题.考查了知识的综合运用,分析推理和基本的运算能力.
 ,
,由条件得
 ,-----------------2分
,-----------------2分即
 动点P的轨迹C的方程为
动点P的轨迹C的方程为 -----------------6分分(注:无x≠0扣1分)
-----------------6分分(注:无x≠0扣1分)(2)设点M,N的坐标分别是(x1,y1),(x2,y2),
ⅰ)当直线l垂直于x轴时,

∴

∴
 ---------------10分
---------------10分ⅱ)当直线l不垂直于x轴时,设直线l的方程为y=k(x+1),
由
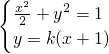 得(1+2k2)x2+4k2x+2k2-2=0----------11分
得(1+2k2)x2+4k2x+2k2-2=0----------11分∴
 ----------------12分
----------------12分∴

又∵y1=k(x1+1),y2=k(x2+1),
∴
 -----------------13分
-----------------13分=
 -------------------14分
-------------------14分综上所述
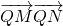 的最大值是
的最大值是 ----------------15分
----------------15分∴λ的最小值为
 -----------------------16分
-----------------------16分分析:(1)设动点P的坐标为(x,y),可表示出直线PA,PB的斜率,根据题意直线PA、PB的斜率之积为
 建立等式求得x和y的关系式,即点P的轨迹方程.
建立等式求得x和y的关系式,即点P的轨迹方程.(2)设点M,N的坐标,当直线l垂直于x轴时,分别表示出
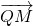 和
和  ,进而可求得
,进而可求得 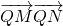 ;再看直线l不垂直于x轴时,设直线l的方程,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而表示出
;再看直线l不垂直于x轴时,设直线l的方程,把直线方程与椭圆方程联立,利用韦达定理表示出x1+x2和x1x2,进而表示出 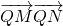 判断出其范围,综合求得
判断出其范围,综合求得 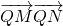 的最大值,根据
的最大值,根据 恒成立,求得λ的最小值.
恒成立,求得λ的最小值.点评:本题主要考查了直线与圆锥曲线的综合问题.考查了知识的综合运用,分析推理和基本的运算能力.

练习册系列答案
相关题目
 已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.
已知点A(0,1),B,C是x轴上两点,且|BC|=6(B在C的左侧).设△ABC的外接圆的圆心为M.