题目内容
(本小题满分12分)已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() ,
,
![]() ;(1)求数列
;(1)求数列![]() 的通项公式
的通项公式
(2)设数列![]() 满足:
满足:![]() ,且
,且![]() ,求证:
,求证:![]() (3)若(2)问中数列
(3)若(2)问中数列![]() 满足
满足 ![]() ,
,
求证: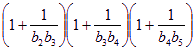
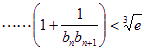 (其中
(其中![]() 为自然对数的底数)。
为自然对数的底数)。
(Ⅰ) 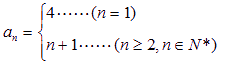 (Ⅱ) 见解析 (Ⅲ)见解析
(Ⅱ) 见解析 (Ⅲ)见解析
解析:
(1)当![]() 时,
时,![]()
两式相减得:![]()
![]() …2分
…2分
![]() 可得:
可得:![]()
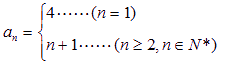 4分
4分
( 2 )、证明: ①当![]() 时,
时,![]() 成立;…… 5分
成立;…… 5分
②假设当 ![]() 时,
时,![]() 成立,即
成立,即 ![]() ,
,
那么,当![]() 时
时
![]() ,
,
所以,当 ![]() 时,
时,![]() 也成立 。… 8分
也成立 。… 8分
根据①,②可知,![]() 。…… 9分
。…… 9分
(3)、证明:设![]() ,
,![]() ,易知,
,易知,
![]() 在
在![]() 上单调递减,所以,当
上单调递减,所以,当 ![]() 时,
时,![]()
因此 ![]()
由⑴、⑵知![]() ,即
,即 ![]() …… 11分
…… 11分
![]()
![]()
![]() 所以,
所以,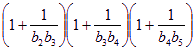
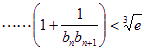 13
13

练习册系列答案
相关题目