题目内容
【题目】以下说法错误的是( )
A.复数![]() 满足
满足![]() ,则复数
,则复数![]() 在复平面上对应的点的轨迹为直线.
在复平面上对应的点的轨迹为直线.
B.![]() 为
为![]() 上连续可导的函数,若
上连续可导的函数,若![]() ,则
,则![]() 为极值点.
为极值点.
C.若![]() ,
,![]() ,
,![]() ,则
,则![]() .
.
D.![]() 为抛物线
为抛物线![]() 的两点,
的两点,![]() 为坐标原点,若
为坐标原点,若![]() ,则直线
,则直线![]() 过定点
过定点![]() .
.
【答案】ABD
【解析】
根据复数的几何意义,可判断A选项;根据函数![]() 的单调性,判断B选项;根据向量模的计算公式,判断C选项;根据直线与抛物线的综合,判断D选项.
的单调性,判断B选项;根据向量模的计算公式,判断C选项;根据直线与抛物线的综合,判断D选项.
对于A选项,设复数![]() ,因为
,因为![]() ,
,
所以![]() ,即
,即![]() ,
,
表示复平面内的点![]() 到定点
到定点![]() ,
,![]() 的距离的和等于定值
的距离的和等于定值![]() (与两定点间的距离相等),因此复数
(与两定点间的距离相等),因此复数![]() 在复平面上对应的点的轨迹为以
在复平面上对应的点的轨迹为以![]() ,
,![]() 为端点的线段,故A错;
为端点的线段,故A错;
对于B选项,若![]() ,则
,则![]() ,由
,由![]() 得,
得,![]() ,但函数
,但函数![]() 在
在![]() 上为增函数,无极值,故B错;
上为增函数,无极值,故B错;
对于C选项,因为![]() ,
,![]() ,
,![]() ,
,
则![]() .故C正确;
.故C正确;
对于D选项,由题意,设![]() ,
,![]() ,直线
,直线![]() 的方程为:
的方程为:![]() (
(![]() ),
),
由 得
得![]() ,所以
,所以![]() ,因此
,因此![]() ,
,
又![]() ,所以
,所以![]() ,即
,即![]() ,即
,即![]() ,
,
所以![]() ;即直线
;即直线![]() 过定点
过定点![]() ,故D错.
,故D错.
故选:ABD

【题目】某县畜牧技术员张三和李四9年来一直对该县山羊养殖业的规模进行跟踪调查,张三提供了该县某山羊养殖场年养殖数量![]() 单位:万只
单位:万只![]() 与相应年份
与相应年份![]() 序号
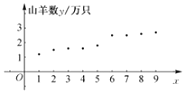
序号![]() 的数据表和散点图
的数据表和散点图![]() 如图所示
如图所示![]() ,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数
,根据散点图,发现y与x有较强的线性相关关系,李四提供了该县山羊养殖场的个数![]() 单位:个
单位:个![]() 关于x的回归方程
关于x的回归方程![]() .
.
年份序号x | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 |
年养殖山羊 |
|
|
|
|
|
|
|
|
|
![]() 根据表中的数据和所给统计量,求y关于x的线性回归方程
根据表中的数据和所给统计量,求y关于x的线性回归方程![]() 参考统计量:
参考统计量:![]() ,
,![]() ;
;
![]() 试估计:
试估计:![]() 该县第一年养殖山羊多少万只
该县第一年养殖山羊多少万只
![]() 到第几年,该县山羊养殖的数量与第一年相比缩小了?
到第几年,该县山羊养殖的数量与第一年相比缩小了?
附:对于一组数据![]() ,
,![]() ,
,![]() ,其回归直线
,其回归直线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为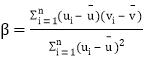 ,
,![]() .
.
【题目】
某位同学进行寒假社会实践活动,为了对白天平均气温与某奶茶店的某种饮料销量之间的关系进行分析研究,他分别记录了1月11日至1月15日的白天平均气温![]() (°C)与该奶茶店的这种饮料销量
(°C)与该奶茶店的这种饮料销量![]() (杯),得到如下数据:
(杯),得到如下数据:
日 期 | 1月11日 | 1月12日 | 1月13日 | 1月14日 | 1月15日 |
平均气温 | 9 | 10 | 12 | 11 | 8 |
销量 | 23 | 25 | 30 | 26 | 21 |
(1)若从这五组数据中随机抽出2组,求抽出的2组数据恰好是相邻2天数据的概率;
(2)请根据所给五组数据,求出y关于x的线性回归方程![]() .
.
(参考公式: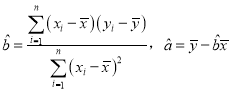 .)
.)