题目内容
已知数列{an}满足:a1=2t,t2-2an-1t+an-1an=0,n=2,3,4,…(其中t为常数,且t≠0),
(Ⅰ)求证:数列 为等差数列;
为等差数列;
(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。
(Ⅰ)求证:数列
 为等差数列;
为等差数列;(Ⅱ)求数列{an}的通项公式;
(Ⅲ)设
 ,求数列{bn}的前n项和Sn。
,求数列{bn}的前n项和Sn。 (Ⅰ)证明:∵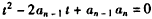 ,
,
∴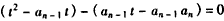 ,
,
∴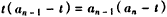 ,
,
由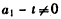 知
知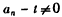 ,
,
∴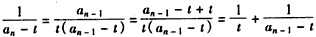 ,
,
即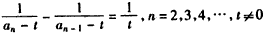 ,
,
∴数列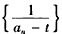 为等差数列。
为等差数列。
(Ⅱ)解:由(Ⅰ)得,数列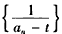 为等差数列,公差为
为等差数列,公差为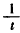 ,
,
∴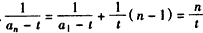 ,
,
∴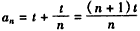 。
。
(Ⅲ)解: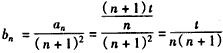
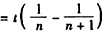 ,
,
∴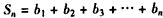
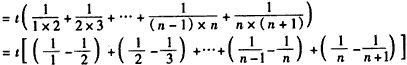
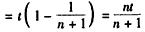 。
。
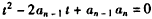 ,
,∴
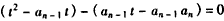 ,
,∴
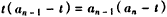 ,
,由
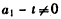 知
知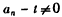 ,
,∴
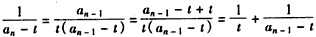 ,
,即
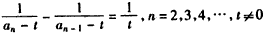 ,
,∴数列
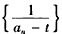 为等差数列。
为等差数列。(Ⅱ)解:由(Ⅰ)得,数列
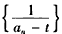 为等差数列,公差为
为等差数列,公差为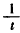 ,
,∴
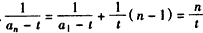 ,
,∴
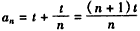 。
。(Ⅲ)解:
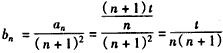
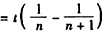 ,
,∴
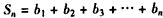
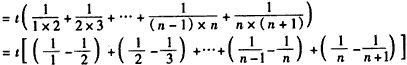
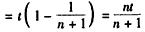 。
。
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目