题目内容
设全集U=Z,集合M={1,2},P={x|-2≤x≤2,x∈Z},则P∩( M)等于( )
M)等于( )
| A.{0} | B.{1} | C.{-2,-1,0} | D.Ø |
C
解析试题分析:根据题意,由于全集U=Z,集合M={1,2},P={x|-2≤x≤2,x∈Z},则根据补集的定义 M={-2,-1,0},因此P∩(
M={-2,-1,0},因此P∩( M)={-2,-1,0},故可知答案为C.
M)={-2,-1,0},故可知答案为C.
考点:集合的运算
点评:主要是考查了集合的基本运算,属于基础题.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
设全集 ,则
,则 ( )
( )
A. | B. | C. | D. |
集合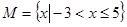 ,
,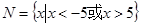 ,则
,则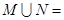 ( )
( )
A.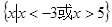 | B.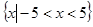 |
C.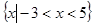 | D.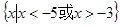 |
已知集合 ,
, ,则
,则
A. | B. | C. | D. |
集合 ,集合
,集合 ,若集合
,若集合 ,则实数
,则实数 的取值范围是
的取值范围是
A. | B. | C. | D. |
已知集合 ,
, ,则
,则 ( ) .
( ) .
A. | B. |
C. | D. |
设集合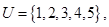 集合
集合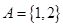 ,则
,则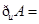 ( )
( )
A.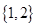 | B.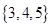 | C.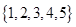 | D.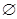 |
已知集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
 ,x∈R},B="{y|" y=x2+1,x∈R},则A∩B为( )
,x∈R},B="{y|" y=x2+1,x∈R},则A∩B为( )  . D.{(0,1)}
. D.{(0,1)}