Question

（本题14分）口袋内有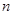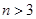（）个大小相同的球，其中有3个红球和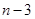个白球．已知从

口袋中随机取出一个球是红球的概率是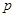，且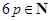。若有放回地从口袋中连续地取四次球（每次只取一个球），在四次取球中恰好取到两次红球的概率大于。

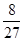（Ⅰ）求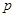和；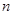

（Ⅱ）不放回地从口袋中取球（每次只取一个球），取到白球时即停止取球，记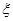为第一次取到白球时的取球次数，求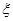的分布列和期望。

 

Answer 1

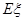【答案】

(1) 和 (2)

【解析】

试题分析：解：（I）由题设知，，

因为所以不等式可化为，

解不等式得，，即．

又因为，所以，即，

所以，所以，所以．   ………………7分

（II）可取1，2，3 ，4

的分布列为

	1	2	3	4
p

．   ……………14分

考点：分布列和数学期望，古典概型

点评：对于概率试题的求解，主要是能对于古典概型的事件空间准确求解，同时能根据各个概率的取值，得到分布列，属于中档题。