题目内容
已知x满足不等式(log2x)2-4log2x+3≤0.
(1)求x的范围;
(2)在(1)的结论下,求f(x)=log2
•log2
的最大值和最小值.
(1)求x的范围;
(2)在(1)的结论下,求f(x)=log2
| x |
| 2 |
| x |
| 4 |
分析:(1)(log2x)2-4log2x+3≤0⇒(log2x-1)(log2x-3)≤0,解此不等式即可求得x的范围;
(2)利用对数的运算性质可得f(x)=(log2x-1)(log2x-2),配方即可求得f(x)的最大值和最小值.
(2)利用对数的运算性质可得f(x)=(log2x-1)(log2x-2),配方即可求得f(x)的最大值和最小值.
解答:解:(1)∵(log2x)2-4log2x+3≤0,
∴(log2x-1)(log2x-3)≤0,
∴1≤log2x≤3,
∴2≤x≤8;
∴x的范围为[2,8];
(2)∵f(x)=log2
•log2
=(log2x-1)(log2x-2)
=(log2x-
)2-
,1≤log2x≤3,
∴当log2x=
时,f(x)取到最小值-
;
当log2x=3时,f(x)取到最大值2.
∴(log2x-1)(log2x-3)≤0,
∴1≤log2x≤3,
∴2≤x≤8;
∴x的范围为[2,8];
(2)∵f(x)=log2
| x |
| 2 |
| x |
| 4 |
=(log2x-1)(log2x-2)
=(log2x-
| 3 |
| 2 |
| 1 |
| 4 |
∴当log2x=
| 3 |
| 2 |
| 1 |
| 4 |
当log2x=3时,f(x)取到最大值2.
点评:本题考查对数不等式的解法,考查等价转化思想与方程思想的综合应用,考查二次函数的配方法,属于中档题.

练习册系列答案
相关题目
 (考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分)
(考生注意:请在下列三题中任选一题作答,如果多做,则按所做的第一题评阅记分) B、
B、
 D、m,n的关系不能确定
D、m,n的关系不能确定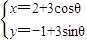 (θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .
(θ为参数),直线l的方程为x-3y+2=0,则曲线C上的动点P(x,y)到直线l距离的最大值为 .