题目内容
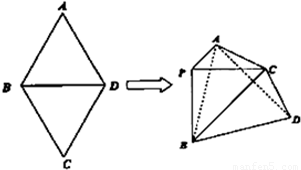
如图，菱形ABCD所在平面与矩形ACEF所在平面相互垂直，点M是线段EF的中点。（1）求证：AM // 平面BDE（6分） （2）当
为何值时，平面DEF
平面BEF？并证明你的结论。（8分）
(Ⅰ) 略 (Ⅱ) 
…
解析:
证明（1）取AC与BD的交点N，连接EN， 1分
由题意知：EN // AM， 4分又EN在平面BDE内， …5分
所以AM // 平面BDE ……6分
（2）当时，平面DEF
平面BEF……7分
因为面ACEF面ABCD，四边形ACEF为矩形，
所以FA、EC都垂直于面ABCD，又四边形ABCD是菱形，
所以
FAD
ECA，所以DF＝DE又M为EF的中点，所以DMEF，………10分
当DMBM时，就有DM平面BEF …12分
即
DMB＝90
时，平面DEF平面BEF ∴……14分
练习册系列答案
相关题目
（2012•闸北区二模）如图，菱形ABCD中，AB=AC=1，其对角线的交点为O，现将△ADC沿对角线AC向上翻折，使得OD⊥OB．在四面体ABCD中，E在AB上移动，点F在DC上移动，且AE=CF=a（0≤a≤1）．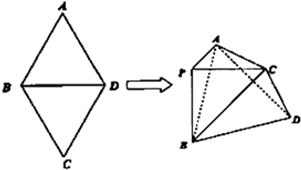
如图，菱形ABCD中，∠A=60°，把菱形ABCD沿对角线BD折成二面角A-BD-C，AC=BD，空间中的点P满足PA、PB、PC两两垂直，则下列命题中错误的是（ ）
