题目内容
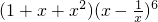的展开式中的常数项为m，则函数y=-x2与y=mx的图象所围成的封闭图形的面积为
- A.
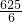
- B.
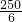
- C.
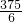
- D.
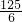
D
分析：由题意，先根据二项展开式的通项求出常数项m，然后利用积分，求得图形的面积即可
解答：
解：由于
的展开式的通项为
=
分别令6-2r=0可得r=3，
=-20
令6-2r=-1，则r不存在
令6-2r=-2可得r=4，
=15x-2
∴m=-20×1+15x-2×x2=-5
∴y=-x2与y=mx=-5x的交点O（0，0），A（5，-25），
图象围成的封闭图形的面积S=
=
=
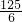
故选D
点评：本题考查定积分在求面积中的应用以及二项式的性质，求解的关键利用二项式定理求出常数项，积分与二项式定理这样结合，形式较新颖，本题易因为对两个知识点不熟悉公式用错而导致错误，牢固掌握好基础知识很重要．
分析：由题意，先根据二项展开式的通项求出常数项m，然后利用积分，求得图形的面积即可
解答：
解：由于的展开式的通项为=分别令6-2r=0可得r=3，
=-20令6-2r=-1，则r不存在
令6-2r=-2可得r=4，
=15x-2∴m=-20×1+15x-2×x2=-5
∴y=-x2与y=mx=-5x的交点O（0，0），A（5，-25），
图象围成的封闭图形的面积S=
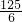
==故选D
点评：本题考查定积分在求面积中的应用以及二项式的性质，求解的关键利用二项式定理求出常数项，积分与二项式定理这样结合，形式较新颖，本题易因为对两个知识点不熟悉公式用错而导致错误，牢固掌握好基础知识很重要．
练习册系列答案
名校课堂系列答案
相关题目
若二项式(a
-
)6的展开式中的常数项为-160，则
(3x2-1)dx= ．
（文科）下表是某厂1～4月份用水量（单位：百吨）的一组数据，
由其散点图可知，用水量y与月份x之间有较好的线性相关关系，其线性回归方程
是 ．
| x |
| 1 | ||
|
| ∫ | a 0 |
（文科）下表是某厂1～4月份用水量（单位：百吨）的一组数据，
| 月 份x | 1 | 2 | 3 | 4 |
| 用水量y | 4.5 | 4 | 3 | 2.5 |
是
”是“sina=1”的充要条件；
+
）4的展开式中的常数项为2；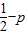
；