题目内容
【题目】选修4-4：坐标系与参数方程
在直角坐标系
中，曲线
的参数方程为
（
为参数），以原点
为极点，
轴的正半轴为极轴，建立极坐标系，曲线
的极坐标方程
；
（Ⅰ）求曲线的普通方程和曲线的直角坐标方程；
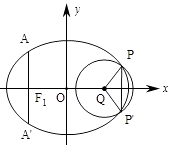
（Ⅱ）设
为曲线上的动点，求点到曲线上的距离的最小值的值.
【答案】(1) 
；
.
(2) 当
时，
的最小值为
.
【解析】分析：（Ⅰ）利用三角函数的基本关系把参数方程化为直角坐标方程，利用直角坐标和极坐标的互化公式
，把极坐标方程化为直角坐标方程；（Ⅱ）求得椭圆上
到直线
的距离为
，可得
的最小值，以及此时的
的值，从而求得点的坐标.
详解：（Ⅰ）由曲线
（为参数），曲线
的普通方程为：.
由曲线
，展开可得：
，化为：.
即：曲线
的直角坐标方程为：.
（Ⅱ）椭圆上的点到直线
的距离为
∴当时，的最小值为
.
练习册系列答案
相关题目
【题目】随机调查
名性别不同的大学生是否喜欢打羽毛球，得到如下
列联表：
男 | 女 | 总计 | |
喜欢打羽毛球 |
|
|
|
不喜欢打羽毛球 |
|
|
|
总计 |
|
|
|
临界值表：
|
|
|
|
|
|
|
|
参考公式：
（其中
）
参照临界值表，下列结论正确的是（ ）
A. 在犯错误的概率不超过
的前提下，认为“喜欢打羽毛球与性别有关”
B. 在犯错误的概率不超过的前提下，认为“喜欢打羽毛球与性别无关”
C. 在犯错误的概率不超过
的前提下，认为“喜欢打羽毛球与性别有关”
D. 在犯错误的概率不超过的前提下，认为“喜欢打羽毛球与性别无关”
