题目内容
(本小题满分12分)
已知函数![]() ,且
,且![]() 。
。
(I)试用含![]() 的代数式表示
的代数式表示![]() ;
;
(Ⅱ)求![]() 的单调区间;
的单调区间;
(Ⅲ)令![]() ,设函数
,设函数![]() 在
在![]() 处取得极值,记点
处取得极值,记点![]() ,证明:线段
,证明:线段![]() 与曲线
与曲线![]() 存在异于
存在异于![]() 、
、![]() 的公共点。
的公共点。
(I)![]()
(Ⅱ)当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调增区间为R;
的单调增区间为R;
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() 。
。
(Ⅲ)证明见解析。
解析:
解法一:
(I)依题意,得![]()
由![]() 得
得![]()
(Ⅱ)由(I)得![]()
故![]()
令![]() ,则
,则![]() 或
或![]()
①当![]() 时,
时,![]()
当![]() 变化时,
变化时,![]() 与
与![]() 的变化情况如下表:
的变化情况如下表:
|
|
|
|
|
|
| + | — | + |
|
| 单调递增 | 单调递减 | 单调递增 |
由此得,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
②由![]() 时,
时,![]() ,此时,
,此时,![]() 恒成立,且仅在
恒成立,且仅在![]() 处
处![]() ,故函数
,故函数![]() 的单调区间为R
的单调区间为R
③当![]() 时,
时,![]() ,同理可得函数
,同理可得函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
综上:
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ;
;
当![]() 时,函数
时,函数![]() 的单调增区间为R;
的单调增区间为R;
当![]() 时,函数
时,函数![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
(Ⅲ)当![]() 时,得
时,得![]()
由![]() ,得
,得![]()
由(Ⅱ)得![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]()
所以函数![]() 在
在![]() 处取得极值。
处取得极值。
故![]()
所以直线![]() 的方程为
的方程为![]()
由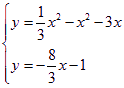 得
得![]()
令![]()
易得![]() ,而
,而![]() 的图像在
的图像在![]() 内是一条连续不断的曲线,
内是一条连续不断的曲线,
故![]() 在
在![]() 内存在零点
内存在零点![]() ,这表明线段
,这表明线段![]() 与曲线
与曲线![]() 有异于
有异于![]() 的公共点
的公共点
解法二:
(I)同解法一
(Ⅱ)同解法一。
(Ⅲ)当![]() 时,得
时,得![]() ,由
,由![]() ,得
,得![]()
由(Ⅱ)得![]() 的单调增区间为
的单调增区间为![]() 和
和![]() ,单调减区间为
,单调减区间为![]() ,所以函数
,所以函数![]() 在
在![]() 处取得极值,
处取得极值,
故![]()
所以直线![]() 的方程为
的方程为![]()
由 得
得![]()
解得![]()
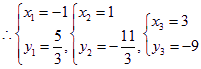
所以线段![]() 与曲线
与曲线![]() 有异于
有异于![]() 的公共点
的公共点![]() 。
。

练习册系列答案
相关题目