题目内容
已知函数f（x）=
+（x-1）0的定义域为M，g（x）=ln（2-x）的定义域为N，则M∩N=
- A.{x|x＞-2}
- B.{x|x＜2}
- C.{x|-2＜x＜2}
- D.以上都不对
D
分析：由题设知M={x|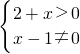
}={x|x＞-2，且x≠1}．N={x|2-x＞0}={x|x＜2}，由此能求出M∩N={x|-2＜x＜2，且x≠1}．
解答：由题设知M={x|}，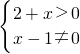
∴M={x|x＞-2，且x≠1}．
N={x|2-x＞0}={x|x＜2}，
M∩N={x|-2＜x＜2，且x≠1}．
故选D．
点评：本题考查函数的定义域及求法，解题时要认真审题，仔细解答，注意集合的交运算．
分析：由题设知M={x|
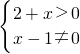}={x|x＞-2，且x≠1}．N={x|2-x＞0}={x|x＜2}，由此能求出M∩N={x|-2＜x＜2，且x≠1}．解答：由题设知M={x|
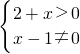}，∴M={x|x＞-2，且x≠1}．
N={x|2-x＞0}={x|x＜2}，
M∩N={x|-2＜x＜2，且x≠1}．
故选D．
点评：本题考查函数的定义域及求法，解题时要认真审题，仔细解答，注意集合的交运算．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
已知函数f（x）=x2-bx的图象在点A（1，f（1））处的切线l与直线3x-y+2=0平行，若数列{
}的前n项和为Sn，则S2010的值为（ ）
| 1 |
| f(n) |
A、
| ||
B、
| ||
C、
| ||
D、
|