题目内容
已知函数f(x)=ln(1+x)-x，g(x)=xlnx，
(1)求函数f(x)的最大值；
(2)设0＜a＜b，证明：0＜g(a)+g(b)-2g(
)＜(b-a)ln2。
(1)求函数f(x)的最大值；
(2)设0＜a＜b，证明：0＜g(a)+g(b)-2g(
)＜(b-a)ln2。(Ⅰ)解：函数f(x)的定义域是(-1，+∞)，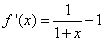
，
令f′(x)=0，解得x=0，
当-1＜x＜0时，f′(x)＞0，当x＞0时，f′(x)＜0，
又f(0)=0，故当且仅当x=0时，f(x)取得最大值，最大值是0。
(Ⅱ)证明：g(a)+g(b)-2g(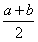
)=alna+blnb-(a+b)ln
=
，
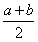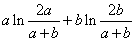由(Ⅰ)的结论知ln(1+x)-x＜0(x＞-1，且x≠0)，
由题设0＜a＜b，得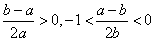
，
因此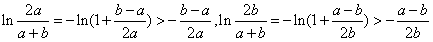
，
所以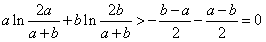
，
又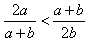
，
，
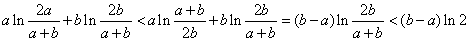综上0＜g(a)+g(b)-2g(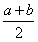
)＜(b-a)ln2。
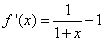，令f′(x)=0，解得x=0，
当-1＜x＜0时，f′(x)＞0，当x＞0时，f′(x)＜0，
又f(0)=0，故当且仅当x=0时，f(x)取得最大值，最大值是0。
(Ⅱ)证明：g(a)+g(b)-2g(
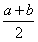)=alna+blnb-(a+b)ln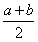=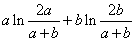，由(Ⅰ)的结论知ln(1+x)-x＜0(x＞-1，且x≠0)，
由题设0＜a＜b，得
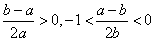，因此
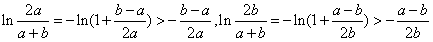，所以
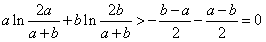，又
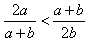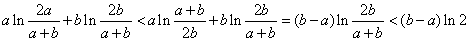，，综上0＜g(a)+g(b)-2g(
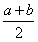)＜(b-a)ln2。
练习册系列答案
相关题目