题目内容
设关于x的方程4x+(a-2)·2x+a2=0有两个相异的正根,求实数a的取值范围.
思路分析:原方程可看成关于2x的“二次”方程,利用二次方程根的知识解决.
解:方法一:令t=2x,原方程化为t2+(a-2)t+a2=0, ①
∵原方程有两个相异正根,
∴关于t方程①有两个大于1的相异根.令f(t)=t2+(a-2)t+a2,考查f(t)的图象,如下图.
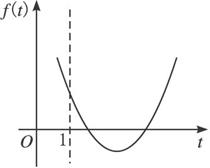
当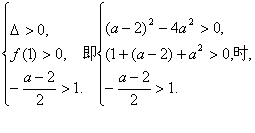
关于t的方程①有两个大于1的相异根,解得-2<a<![]() .
.
∴a的取值范围为{a|-2<a<![]() }.
}.
方法二:令t=2x,原方程化为
t2+(a-2)t+a2=0, ①
∵原方程有两个相异正根,
∴关于t的方程①有两个大于1的相异根,设为t1,t2,
∵t1>1,t2>1,
∴t1-1>0,t2-1>0.
∴(t1-1)+(t2-1)=t1+t2-2=-(a-2)-2=-a>0,
(t1-1)·(t2-1)=t1·t2-(t1+t2)+1=a2+a-2+1>0.
∴方程①有两个大于1的相异正根的充要条件为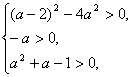
解得-2<a<![]() .
.
∴a的取值范围为{a|-2<a<![]() }.
}.

练习册系列答案
相关题目