题目内容
已知A、B是互相独立事件,C与A,B分别是互斥事件,已知P(A)=0.2,P(B)=0.6,P(C)=0.14,则A、B、C至少有一个发生的概率P(A+B+C)= .
【答案】分析:先求得A、B、C中只有一种发生的概率是0.2×0.4+0.8×0.6+0.14=0.7,而A、B、C中发生两种的概率(只能是A、B)为 0.2×0.6=0.12,相加,即得所求.
解答:解:A、B、C中只有一种发生的概率是0.2×0.4+0.8×0.6+0.14=0.7,
A、B、C中发生两种的概率(只能是A、B)为 0.2×0.6=0.12,不可能3种都发生,
所以,A、B、C至少发生一件的概率为0.7+0.12=0.82.
A、B、C至少有一个发生的概率P(A+B+C)=0.7+0.12=0.82,
故答案为 0.82.
点评:本题主要考查相互独立事件的概率乘法公式,属于中档题.
解答:解:A、B、C中只有一种发生的概率是0.2×0.4+0.8×0.6+0.14=0.7,
A、B、C中发生两种的概率(只能是A、B)为 0.2×0.6=0.12,不可能3种都发生,
所以,A、B、C至少发生一件的概率为0.7+0.12=0.82.
A、B、C至少有一个发生的概率P(A+B+C)=0.7+0.12=0.82,
故答案为 0.82.
点评:本题主要考查相互独立事件的概率乘法公式,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 且互相独立,灯亮的概率为 ( )。
且互相独立,灯亮的概率为 ( )。  B、
B、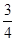 C、
C、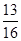 D、
D、

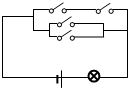 如图,已知电路中4个开关闭合的概率都是
如图,已知电路中4个开关闭合的概率都是 且互相独立,灯亮的概率为
且互相独立,灯亮的概率为


