题目内容
(12分)设函数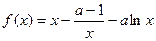
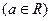 .
.
(I)若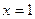 是函数
是函数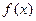 的极大值点,求
的极大值点,求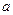 的取值范围;
的取值范围;
(II)当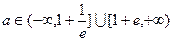 时,若在
时,若在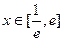 上至少存在一点
上至少存在一点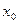 ,使
,使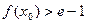 成立,求
成立,求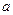 的取值范围.
的取值范围.
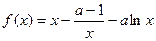
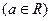 .
.(I)若
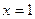 是函数
是函数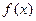 的极大值点,求
的极大值点,求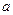 的取值范围;
的取值范围;(II)当
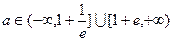 时,若在
时,若在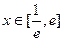 上至少存在一点
上至少存在一点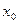 ,使
,使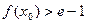 成立,求
成立,求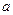 的取值范围.
的取值范围.(I)当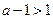 ,即
,即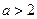 时,
时,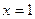 是函数
是函数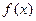 的极大值点.
的极大值点.
(II)当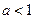 时,在
时,在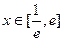 上至少存在一点
上至少存在一点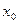 ,使
,使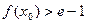 .
.
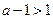 ,即
,即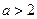 时,
时,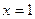 是函数
是函数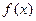 的极大值点.
的极大值点.(II)当
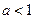 时,在
时,在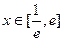 上至少存在一点
上至少存在一点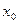 ,使
,使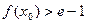 .
.解: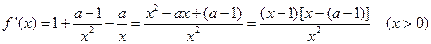 …1分
…1分
当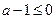 时,
时,
当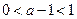 时,
时,
当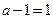 时,
时,
当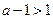 时,
时,
综上所述,当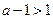 ,即
,即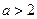 时,
时,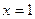 是函数
是函数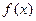 的极大值点.………………6分
的极大值点.………………6分
(2)问题等价于当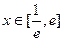 时,
时,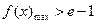 .………………7分
.………………7分
由(1)知,①当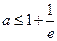 ,即
,即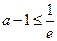 时,函数
时,函数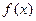 在
在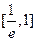 上递减,在
上递减,在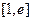 上递增,
上递增,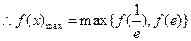 .由
.由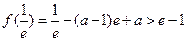 ,解得
,解得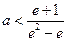 .由
.由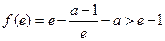 ,解得
,解得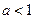
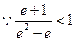 ,
,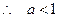 ;………………9分
;………………9分
②当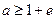 ,即
,即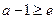 时,函数
时,函数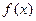 在
在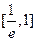 上递增,在
上递增,在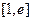 上递减,
上递减,
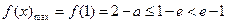 .………………11分
.………………11分
综上所述,当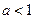 时,在
时,在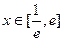 上至少存在一点
上至少存在一点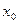 ,使
,使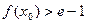 成立…12分
成立…12分
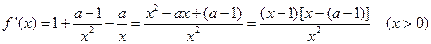 …1分
…1分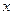 | 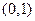 |  | 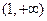 |
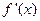 |  |  | 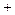 |
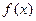 | 递减 | 极小值 | 递增 |
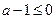 时,
时,当
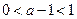 时,
时,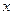 | 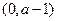 | 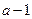 | 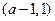 | 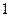 | 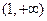 |
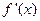 | 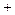 | 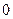 | 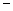 | 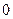 | 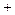 |
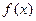 | 递增 | 极大值 | 递减 | 极小值 | 递增 |
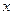 | 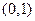 | 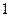 | 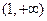 |
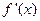 | 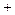 |  | 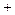 |
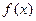 | 递增 | 非极值 | 递增 |
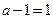 时,
时,当
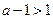 时,
时,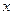 | 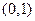 | 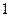 | 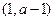 | 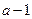 | 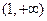 |
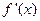 | 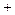 | 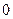 | 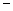 | 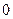 | 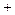 |
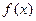 | 递增 | 极大值 | 递减 | 极小值 | 递增 |
综上所述,当
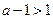 ,即
,即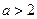 时,
时,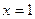 是函数
是函数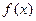 的极大值点.………………6分
的极大值点.………………6分(2)问题等价于当
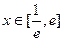 时,
时,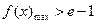 .………………7分
.………………7分由(1)知,①当
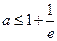 ,即
,即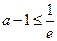 时,函数
时,函数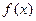 在
在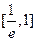 上递减,在
上递减,在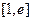 上递增,
上递增,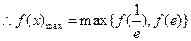 .由
.由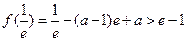 ,解得
,解得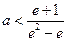 .由
.由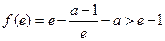 ,解得
,解得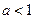
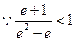 ,
,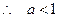 ;………………9分
;………………9分②当
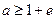 ,即
,即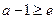 时,函数
时,函数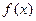 在
在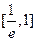 上递增,在
上递增,在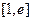 上递减,
上递减,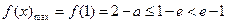 .………………11分
.………………11分综上所述,当
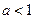 时,在
时,在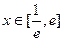 上至少存在一点
上至少存在一点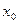 ,使
,使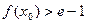 成立…12分
成立…12分
练习册系列答案
相关题目
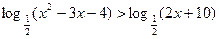 },
},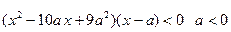 },求M∩N≠
},求M∩N≠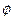 时a的取值范围.
时a的取值范围. 分)
分) ,求
,求 的值域。
的值域。 的定义域为
的定义域为  (B)
(B) (C)
(C) (D)
(D)
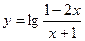 的定义域是 .
的定义域是 .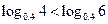 B
B
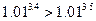 C.
C.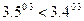 D.
D.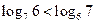
 ,则( ).
,则( ).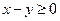



 ,若
,若 ,则
,则


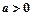 且
且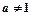 时,函数
时,函数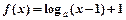 的图像恒过点
的图像恒过点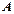 ,若点
,若点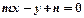 上,则
上,则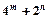 的最小值为____ ____.
的最小值为____ ____.