题目内容
已知正六边形ABCDEF的边长为1,则 的值为( )
的值为( )
A. | B. | C. | D. |
D
解析试题分析:由正六边形的性质可知 ,
, ,代入向量的数量积的运算可知
,代入向量的数量积的运算可知 ,故选D.
,故选D.
考点:本试题主要考查了向量的数量积的运算.
点评:解题的关键是熟练应用正六边形的性质.

练习册系列答案
相关题目
已知 为等边三角形,
为等边三角形,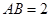 ,设
,设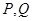 满足
满足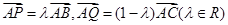 ,若
,若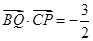 ,则
,则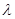 等于( )
等于( )
A.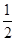 | B.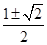 | C.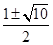 | D.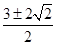 |
化简下列式子:其结果为零向量的个数是( )
① ; ②
; ② ;
;
③ ; ④
; ④
| A.1 | B.2 | C.3 | D.4 |
设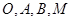 为平面上四点,
为平面上四点,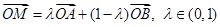 ,则
,则
A.点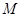 在线段 在线段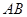 上 上 | B.点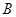 在线段 在线段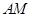 上 上 |
C.点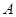 在线段 在线段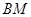 上 上 | D.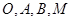 四点共线 四点共线 |
如图,将两全等的等腰直角三角形拼在一起,若 则
则 的值分别为( )
的值分别为( )
A. | B. |
C. | D. |
若 为
为 所在平面内一点,且满足
所在平面内一点,且满足 ,
, ,则
,则 ABC的形状为
ABC的形状为
| A.正三角形 | B.直角三角形 | C.等腰三角形 | D.等腰直角三角形 |
在△ 中,若
中,若 ,则△
,则△ 是( )
是( )
| A.等边三角形 | B.锐角三角形 | C.钝角三角形 | D.直角三角形 |
设O是正方形ABCD的中心,向量 是 ( )
是 ( )
| A.平行向量 | B.有相同终点的向量 | C.相等向量 | D.模相等的向量 |
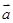 -
-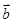 等于 ( )
等于 ( ) 



