题目内容

已知函f（x）是可导函数，且f′（a）=1，则
lim
x→a
f(x)-f(a)
2(x-a)
等于
 
．
分析：利用导数的定义，函数在某点处的导数，就是在该点处函数的增量与自变量的增量的比，求出f′（a），再根据
lim
x→a
f(x)-f(a)
2(x-a)
与f′（a）的关系，求出
lim
x→a
f(x)-f(a)
2(x-a)
解答：解：∵f′（a）=
lim
x→a
f(x)-f(a)
(x-a)
=1
又∴
lim
x→a
f(x)-f(a)
2(x-a)
=
1
2
lim
x→a
f(x)-f(a)
(x-a)
=
1
2
f′（a）=
1
2

故答案为
1
2
点评：本题考查了导数的定义，属于概念考查题．
练习册系列答案
相关题目
函数y=kx+b，其中k，b是常数，其图象是一条直线，称这个函数为线性函数，而对于非线性可导函数f（x），在已知点x0附近一点x的函数值f（x）可以用下面方法求其近似代替值，f（x），利≈f（x0）+f′（x0）（x-x0）用这一方法，对于实数m=
4.002
，取x0的值为4，则m的近似代替值是
2.005
2.005
．
函数y=kx+b，其中k，b（k≠0）是常数，其图象是一条直线，称这个函数为线性函数．而对于非线性可导函数f（x），在已知点
x0附近一点x的函数值f（x），可以用如下方法求其近似代替值：f（x）≈f（x0）+f′（x0）（x-x0）．利用这一方法，对于实数
m=
3.998
，取x0=4，则m的近似代替值
＞
＞
m．（填“＞”或“＜”或“=”）
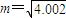函数y=kx+b，其中k，b是常数，其图象是一条直线，称这个函数为线性函数，而对于非线性可导函数f（x），在已知点x附近一点x的函数值f（x）可以用下面方法求其近似代替值，f（x），利≈f（x）+f′（x）（x-x0）用这一方法，对于实数，取x的值为4，则m的近似代替值是    ．
已知函f（x）是可导函数，且f′（a）=1，则等于    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网