题目内容
一个几何体的三视图如图所示，其中正视图是一个等腰直角三角形，侧视图和俯视图均为正三角形，该几何体的体积是分析：由已知中几何体的三视图中，正视图是一个等腰直角三角形，侧视图和俯视图均为正三角形，我们求出该几何体的底面面积和高，代入棱锥体积公式，即可得到答案．
解答：解：由已知中正视图是一个等腰直角三角形
可得该几何体是一个高H为
，底面高也为
的三棱锥
又由俯视图为正三角形，则底面棱长为2，
则底面面积S=
•2•
=
则几何体的体积V=
•S•H=
•
•
=1
故答案为：1
可得该几何体是一个高H为
| 3 |
| 3 |
又由俯视图为正三角形，则底面棱长为2，
则底面面积S=
| 1 |
| 2 |
| 3 |
| 3 |
则几何体的体积V=
| 1 |
| 3 |
| 1 |
| 3 |
| 3 |
| 3 |
故答案为：1
点评：本题考查的知识点是由三视图求体积，其中根据三视图判断出几何体的形状，分析出几何体的几何特征，进而求出底面面积，高是解答本题的关键．
练习册系列答案
相关题目
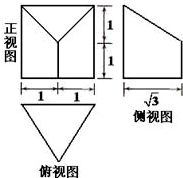
（2013•房山区二模）一个几何体的三视图如图所示，则这个几何体的表面积为（ ）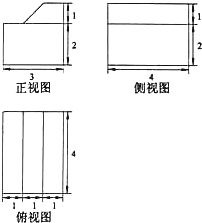
（2012•天津）一个几何体的三视图如图所示（单位：m），则该几何体的体积为
一个几何体的三视图如图所示，其中正视图是一个正三角形，则这个几何体的表面积为
（2010•河东区一模）一个几何体的三视图如图所示，则该几何体（不考虑接触点）的表面积为