题目内容
如图，平面内有三个向量| OA |
| OB |
| OC |
| OA |
| OB |
| OA |
| OC |
| OA |
| OB |
| OC |
| 3 |
| OC |
| OA |
| OB |
2
-3
| 3 |
2
-3
．| 3 |
分析：先利用向量加法的平行四边形法则，将
表示为
与
的和，再利用解直角三角形知识，计算OD、OE的长，即可得λ和μ的值
| OC |
| OD |
| OE |
解答：解：如图：
过C分别作OA、OB的平行线交OB、OA于E、D，则四边形EODC为平行四边形，
在△COD中，OC=2
，∠COD=60°，∠OCD=∠EOC=90°，∴OD=2OC=4
，而OA=2，∴
=2
在△COE中，OC=2
，∠OCE=60°，∠EOC=90°，∴OE=OCtan60°=6，而OB=2，∴
=3
∴
=
+
=2
+3
∴λ=2
，μ=3
∴λ-μ=2
-3
故答案为 2
-3
过C分别作OA、OB的平行线交OB、OA于E、D，则四边形EODC为平行四边形，在△COD中，OC=2
| 3 |
| 3 |
| OD |
| 3 |
| OA |
在△COE中，OC=2
| 3 |
| OE |
| OB |
∴
| OC |
| OD |
| OE |
| 3 |
| OA |
| OB |
∴λ=2
| 3 |
∴λ-μ=2
| 3 |
故答案为 2
| 3 |
点评：本题主要考查了平面向量的基本定理，向量加法的平行四边形法则，实数与向量积的意义，解直角三角形的基础知识，属基础题
练习册系列答案
阅读快车系列答案
相关题目
如图，设Ox，Oy是平面内相交成60°角的两条数轴，
，
分别是与x轴，y轴正方向同向的单位向量，若向量
=x
+y
，则把有序数对（x，y）叫做向量
在坐标系xOy中的坐标．设
，
，给出下列三个命题：
=（1，0）；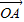
⊥
；
．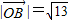