题目内容
函数f(x)=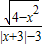 的图象关于( )
的图象关于( )A.y轴对称
B.直线y=x对称
C.坐标原点对称
D.x轴对称
【答案】分析:先求函数的定义域,然后去掉绝对值符号,再判断其奇偶性即可.
解答:解:∵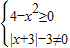 ,解得-2≤x≤2且x≠0,∴函数f(x)=
,解得-2≤x≤2且x≠0,∴函数f(x)=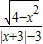 的定义域为{x|-2≤x≤2,且x≠0},可知此定义域关于原点对称.
的定义域为{x|-2≤x≤2,且x≠0},可知此定义域关于原点对称.
∴x+3>0,∴|x+3|=x+3.
∴f(x)=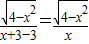 .
.
∴f(-x)=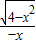 =-f(x),
=-f(x),
∴函数f(x)是奇函数,
∴函数f(x)的图象关于原点对称.
故选C.
点评:正确求出函数的定义域并进行化简与掌握函数的奇偶性的判定方法是解题的关键.
解答:解:∵
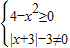 ,解得-2≤x≤2且x≠0,∴函数f(x)=
,解得-2≤x≤2且x≠0,∴函数f(x)=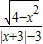 的定义域为{x|-2≤x≤2,且x≠0},可知此定义域关于原点对称.
的定义域为{x|-2≤x≤2,且x≠0},可知此定义域关于原点对称.∴x+3>0,∴|x+3|=x+3.
∴f(x)=
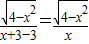 .
.∴f(-x)=
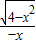 =-f(x),
=-f(x),∴函数f(x)是奇函数,
∴函数f(x)的图象关于原点对称.
故选C.
点评:正确求出函数的定义域并进行化简与掌握函数的奇偶性的判定方法是解题的关键.

练习册系列答案
 轻巧夺冠周测月考直通中考系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目