题目内容
若函数y=f(x)的图象与y=2x的图象关于y轴对称,若y=f-1(x)是y=f(x)的反函数,则y=f-1(x2-2x)的单调递增区间是
- A..[1,+∞)
- B..(2,+∞)
- C..(-∞,1]
- D.(-∞,0)
D
分析:先根据代入求出函数y=f(x)的解析式,从而得到反函数y=f-1(x),求出y=f-1(x2-2x)的解析式,然后求出定义域,在定义域内求内函数的减区间即可.
解答:取函数y=f(x)的图象上任意一点(x,y),则关于y轴对称的点为(-x,y)
根据题意可知点(-x,y)在y=2x的图象上则y=2-x即f(x)=2-x
而y=f-1(x)是y=f(x)的反函数则f-1(x)=
∴y=f-1(x2-2x)=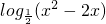
∵x2-2x>0∴x>2或x<0即y=f-1(x2-2x)的定义域为(-∞,0)∪(2,+∞)
y=f-1(x2-2x)的单调递增区间即为x2-2x在定义域(-∞,0)∪(2,+∞)内的减区间
∴y=f-1(x2-2x)的单调递增区间(-∞,0)
故选D.
点评:本题主要考查了函数的对称以及反函数,函数的单调性和函数的定义域,属于易错题,往往不求定义域.
分析:先根据代入求出函数y=f(x)的解析式,从而得到反函数y=f-1(x),求出y=f-1(x2-2x)的解析式,然后求出定义域,在定义域内求内函数的减区间即可.
解答:取函数y=f(x)的图象上任意一点(x,y),则关于y轴对称的点为(-x,y)
根据题意可知点(-x,y)在y=2x的图象上则y=2-x即f(x)=2-x
而y=f-1(x)是y=f(x)的反函数则f-1(x)=

∴y=f-1(x2-2x)=
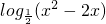
∵x2-2x>0∴x>2或x<0即y=f-1(x2-2x)的定义域为(-∞,0)∪(2,+∞)
y=f-1(x2-2x)的单调递增区间即为x2-2x在定义域(-∞,0)∪(2,+∞)内的减区间
∴y=f-1(x2-2x)的单调递增区间(-∞,0)
故选D.
点评:本题主要考查了函数的对称以及反函数,函数的单调性和函数的定义域,属于易错题,往往不求定义域.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目