题目内容
在△ABC中，a，b，c分别是角A，B，C的对边，
，则
=
- A.
- B.
- C.
- D.
D
分析：利用正弦定理化简已知的等式，再利用同角三角函数间的基本关系变形，求出sinA与sinB的比值，再利用正弦定理即可求出所求式子的值．
解答：在△ABC中，∵，利用正弦定理可得 得：sin2AsinB+sinBcos2A=sinA，
整理得：sinB（sin2A+cos2A）=sinB=sinA，即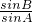 
=，
则由正弦定理得：==，
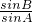故选D．
点评：此题考查了正弦定理，正弦定理很好的建立了三角形的边角关系，熟练掌握正弦定理是解本题的关键，属于中档题．
分析：利用正弦定理化简已知的等式，再利用同角三角函数间的基本关系变形，求出sinA与sinB的比值，再利用正弦定理即可求出所求式子的值．
解答：在△ABC中，∵
，利用正弦定理可得 得：sin2AsinB+sinBcos2A=sinA，整理得：sinB（sin2A+cos2A）=sinB=
sinA，即 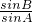=，则由正弦定理得：
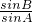==，故选D．
点评：此题考查了正弦定理，正弦定理很好的建立了三角形的边角关系，熟练掌握正弦定理是解本题的关键，属于中档题．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
在△ABC中，∠A、∠B、∠C所对的边长分别是a、b、c．满足2acosC+ccosA=b．则sinA+sinB的最大值是（ ）
A、
| ||||
| B、1 | ||||
C、
| ||||
D、
|