Question

已知二次函数f(x)=ax²+bx+c,当x=-1,0,1时，|f(x)|≤1,求证：当-1≤x≤1时|f(x)|≤.〔揭示：考虑用f(0),f(1),f(-1)表示a、b、c〕

Answer 1

证明：由f(-1)=a-b+c,f(1)=a+b+c,f(0)=c,

由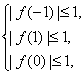即|a-b+c|≤1,|a+b+c|≤1,|c|≤1.

由已知得a=［f(1)+f(-1)-2f(0)］,b=［f(1)-f(-1)］,c=f(0).

于是f(x)= x·(x+1)·f(1)+ x·(x-1)·f(-1)+(1-x²)·f(0).

故|f(x)|≤|x|(x+1)+|x|(1-x)+(1-x²)=-x²+|x|+1≤,

即当-1≤x≤1时，|f(x)|≤.