题目内容
设{an}是公比不为1的等比数列,它的首项为1,且满足an=(1)求{an}的公比的值;
(2)求数列{nan}的前n项和Tn.
解:(1)由题意,2an=an-1+an-2,2q2=q+1,q=-![]() 或1(舍去).∴q=-
或1(舍去).∴q=-![]() .
.
(2)an=(-![]() )n-1.
)n-1.
Tn=1+2·(-![]() )+3·(-
)+3·(-![]() )2+4·(-
)2+4·(-![]() )3+…+(n-1)(-
)3+…+(n-1)(- ![]() )n-2+n·(-
)n-2+n·(-![]() )n-1. ①
)n-1. ①
(-![]() )Tn=(-
)Tn=(-![]() )+2·(-
)+2·(-![]() )2+3·(-
)2+3·(-![]() )3+…+(n-1)(-
)3+…+(n-1)(- ![]() )n-1+n·(-
)n-1+n·(-![]() )n. ②
)n. ②
①-②得,![]() Tn=1+(-
Tn=1+(-![]() )+(-
)+(-![]() )2+…+(-
)2+…+(-![]() )n-1-n·(-
)n-1-n·(-![]() )n,
)n,
![]() =
=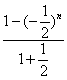
![]() .
.
∴Tn=![]() (-
(-![]() )n-
)n-![]() n(-
n(-![]() )n.
)n.

练习册系列答案
相关题目