题目内容
【题目】已知数列{an}，a1=a（a∈R），an+1= 
（n∈N*）．
（1）若数列{an}从第二项起每一项都大于1，求实数a的取值范围；
（2）若a=﹣3，记Sn是数列{an}的前n项和，证明：Sn＜n+ 
．
【答案】
（1）解：数列{an}从第二项起每一项都大于1，可得
当n≥2时，an+1= 
=2﹣ 
＞2﹣ 
=1，
所以只需a2= 
＞1，解得a＞1或a＜﹣2
（2）证明：由（1）可得，当n≥2时，an+1﹣1= ﹣1
= 
＜ 
= 
（an﹣1），
即有当n≥4时，an﹣1＜（a3﹣1）（ ）n﹣3，
即有an＜1+（a3﹣1）（ ）n﹣3=1+ 
（ ）n﹣3，
此时Sn＜﹣3+5+（1+ ）+[1+ （ ）]+…+[1+ （ ）n﹣3]
=n+ 
=n+ 
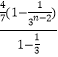[1﹣（ ）n﹣2]＜n+ ，
易证，当n=1，2，3，Sn＜n+ 成立．
综上可得，对任意的正整数n，均有Sn＜n+
【解析】（1）由题意可得当n≥2时，an+1= 
=2﹣ ＞2﹣ =1，所以只需a2= ＞1，解不等式即可得到所求范围；（2）求得当n≥4时，an﹣1＜（a3﹣1）（ ）n﹣3 ， 即有an＜1+（a3﹣1）（ ）n﹣3=1+ （ ）n﹣3 ， 运用等比数列的求和公式和不等式的性质，可得Sn＜n+ ；再验证n=1，2，3也成立．
【考点精析】解答此题的关键在于理解数列的前n项和的相关知识，掌握数列{an}的前n项和sn与通项an的关系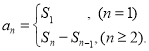
，以及对数列的通项公式的理解，了解如果数列an的第n项与n之间的关系可以用一个公式表示，那么这个公式就叫这个数列的通项公式．
练习册系列答案
相关题目
