题目内容
已知函数f（x）=cos2x-2asinx（0≤x≤π），求f（x）的最值．
解：f（x）=cos2x-2asinx=-sin2x-2asinx+1
令t=sinx，因为0≤x≤π，所以0≤t≤1且y=-t2-2at+1=-（t+a）2+2，其对称轴为t=-a，
故-a≤0时，即a≥0时，y=-t2-2at+1在[0，1]上是减函数，最大值为1；最小值为：-2a，
当0＜-a＜
时，即
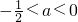时，当t=-a，y有最大值1+a2，最小值为：-2a；
当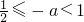
时，即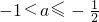
时，当t=-a时y有最大值1+a2，最小值为：1；
当-a≥1时，即a≤-1时，y=-t2-2at+1在[0，1]上是增函数，最小值为1；最大值-2a．
分析：因为cos2x=1-sin2x，用换元法转化为二次函数在特定区间上的最值问题，按照对称轴在区间的左面、在区间内和在区间的右面三种情况讨论．
点评：本题考查三角函数的最值问题，二次函数在特定区间上的最值问题，分类讨论思想和换元转换思想．
令t=sinx，因为0≤x≤π，所以0≤t≤1且y=-t2-2at+1=-（t+a）2+2，其对称轴为t=-a，
故-a≤0时，即a≥0时，y=-t2-2at+1在[0，1]上是减函数，最大值为1；最小值为：-2a，
当0＜-a＜
时，即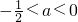时，当t=-a，y有最大值1+a2，最小值为：-2a；当
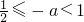时，即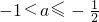时，当t=-a时y有最大值1+a2，最小值为：1；当-a≥1时，即a≤-1时，y=-t2-2at+1在[0，1]上是增函数，最小值为1；最大值-2a．
分析：因为cos2x=1-sin2x，用换元法转化为二次函数在特定区间上的最值问题，按照对称轴在区间的左面、在区间内和在区间的右面三种情况讨论．
点评：本题考查三角函数的最值问题，二次函数在特定区间上的最值问题，分类讨论思想和换元转换思想．
练习册系列答案
阅读快车系列答案
相关题目
已知函数f（x）=
，则关于x的方程f2（x）+bf（x）+c=0有5个不同实数解的充要条件是（ ）
|
| A、b＜-2且c＞0 |
| B、b＞-2且c＜0 |
| C、b＜-2且c=0 |
| D、b≥-2且c=0 |
已知函数f（x）的图象如图所示，则函数的值域为（ ）