题目内容
已知数列{an}是等差数列,设bn=an+12-an2.(1)求证:数列{bn}是等差数列;
(2)若an=-n+2,cn=![]() ,求数列{cn}的前n项和Sn.
,求数列{cn}的前n项和Sn.
(1)证明:设数列{an}的公差为d,则bn+1-bn
=(an+22-an+12)-(an+12-an2)
=(an+2-an+1)(an+2+an+1)-(an+1-an)(an+1+an)
=d(an+2+an+1-an+1-an)
=d(an+2-an)
=2d2为常数.
∴数列{bn}是等差数列.
(2)解:∵an=-n+2,
∴公差d=an+1-an=-1.
∴数列{bn}的公差为2.
∴bn=b1+2·(n-1)=a22-a12+2n-2=2n-3.
∴cn=![]() .
.
∴Sn=![]() ①
①
![]() ②
②
①-②得
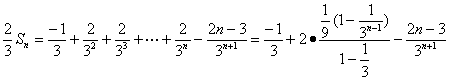
=![]()
∴Sn=![]()

练习册系列答案
相关题目