题目内容
已知两曲线f(x)=cosx,g(x)=sin2x,x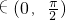 .
.
(1)求两曲线的交点坐标;
(2)设两曲线在交点处的切线分别与x轴交于A,B两点,求AB的长.
解:(1)由cosx=sin2x,得cosx=2sinxcosx,
∵x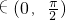 .
.
∴cosx≠0,∴sinx=
∴x= ,f(x)=cos
,f(x)=cos =
=
∴两曲线的交点坐标为( ,
, )
)
(2)∵f′(x)=-sinx
∴f′( )=-
)=-
∴曲线f(x)在交点处的切线方程为y- =-
=- (x-
(x- )
)
∴A( +
+ ,0)
,0)
∵g′(x)=2cos2x
∴g′( )=1
)=1
∴曲线f(x)在交点处的切线方程为y- =x-
=x-
∴B( -
- ,0)
,0)
∴AB= +
+ -
- +
+ =
=
分析:(1)令f(x)=g(x),利用二倍角公式解三角方程即可得交点横坐标,再代入函数解析式计算纵坐标即可
(2)利用导数的几何意义,先分别计算两条曲线的在交点处的切线方程,从而得其与x轴交点A,B的坐标,最后计算两点距离即可
点评:本题考察了导数的几何意义,求曲线切线方程的方法,能解简单的三角方程,会利用二倍角公式化简三角式
∵x
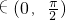 .
.∴cosx≠0,∴sinx=

∴x=
 ,f(x)=cos
,f(x)=cos =
=
∴两曲线的交点坐标为(
 ,
, )
) (2)∵f′(x)=-sinx
∴f′(
 )=-
)=-
∴曲线f(x)在交点处的切线方程为y-
 =-
=- (x-
(x- )
)∴A(
 +
+ ,0)
,0)∵g′(x)=2cos2x
∴g′(
 )=1
)=1∴曲线f(x)在交点处的切线方程为y-
 =x-
=x-
∴B(
 -
- ,0)
,0)∴AB=
 +
+ -
- +
+ =
=
分析:(1)令f(x)=g(x),利用二倍角公式解三角方程即可得交点横坐标,再代入函数解析式计算纵坐标即可
(2)利用导数的几何意义,先分别计算两条曲线的在交点处的切线方程,从而得其与x轴交点A,B的坐标,最后计算两点距离即可
点评:本题考察了导数的几何意义,求曲线切线方程的方法,能解简单的三角方程,会利用二倍角公式化简三角式

练习册系列答案
相关题目
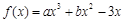
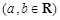 ,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.
,f '(x)为f(x)的导函数,若f '(x)是偶函数且f '(1)=0.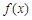 的解析式;
的解析式;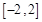 上任意两个自变量的值
上任意两个自变量的值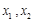 ,都有
,都有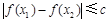 ,求实数
,求实数 的最小值;
的最小值;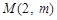
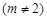 ,可作曲线
,可作曲线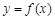 的三条切线,求实数
的三条切线,求实数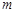 的取值范围.
的取值范围.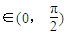 .
.